Řešit Rovnice Numericky

Najít Všechny Kořeny Polynomu Funkce

Použití vpasolve najít všechna řešení, aby funkce f(x)=6×7-2×6+3×3-8.

syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)

vpasolve vrátí sedm kořeny funkce, jak se očekávalo, protože funkce je polynom stupně sedm.,

Nalézt Nuly na Nonpolynomial Funkce Pomocí Vyhledávací Rozsahy a Výchozí Body

graf funkce f(x)=e(x/7)cos(2x) odhaluje pravidelné nul, s rostoucí svahy na nulové body, když x roste.

syms xh = fplot(exp(x/7)*cos(2*x),);grid on

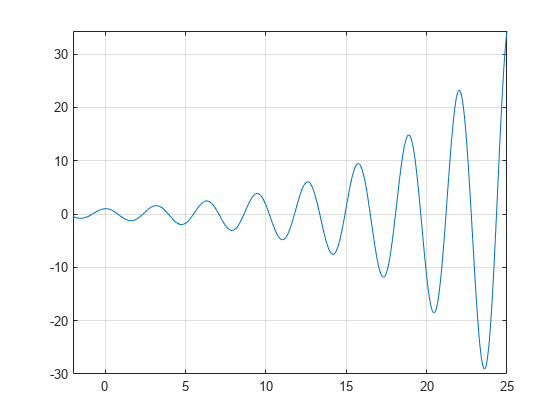
Použití vpasolve najít žádné funkce f. Všimněte si, že vpasolve vrací pouze jedno řešení nepolynomiální rovnice, i když existuje více řešení., On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3 vpasolve(f,x,'Random',true)end

ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')

ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')

ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')

To find a zero close to x=10, set the starting point to 10.,

vpasolve(f,x,10)

ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')

najít žádné blízko x=1000, nastavte počáteční bod 1000.

vpasolve(f,x,1000)

ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')

najít žádné v rozmezí 15≤x≤25, nastavit rozsah hledání .,

vpasolve(f,x,)

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

najít více nul v rozmezí , nelze volat vpasolve opakovaně, protože se to vrátí stejný výsledek na každý hovor, jak již bylo ukázáno. Místo toho nastavte rozsah vyhledávání a nastavte 'Random' na true.,

for k = 1:3 vpasolve(f,x,,'Random',true)end

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')

, Protože 'Random' vybere výchozí body náhodně, stejné řešení může být nalezeno na sobě volání.,

Najít Všechny Nuly v Zadaný Rozsah Hledání

Vytvořit funkci findzeros systematicky najít všechny nuly f v daném vyhledávací rozsah, v určitou chybovou tolerancí. Funkce začíná rozsahem vyhledávání vstupů a volá vpasolve najít nulu. Poté rozdělí rozsah vyhledávání na dvě kolem nulové hodnoty a rekurzivně se nazývá novými rozsahy vyhledávání jako vstupy, aby našel více nul.

funkce je zde vysvětlena.,

deklarujte funkci třemi vstupy a jedním výstupem. První vstup je funkce, druhý vstup je rozsah, a volitelný třetí vstup umožňuje určit chyby mezi nulovou a vyšší a dolní meze generovaných z něj.

function sol = findzeros(f,range,err)

Pokud nechcete zadat volitelný argument pro chyby tolerance, findzeros nastaví err 0.001.

if nargin < 2 err = 1e-3;end

najděte nulu ve vyhledávacím rozsahu pomocí vpasolve.,

sol = vpasolve(f,range);

Pokud vpasolve nenajde žádné, konec.

if(isempty(sol)) return

Pokud vpasolve najde nula, split rozsah vyhledávání do dvou vyhledat pohybuje nad a pod nulou.

else lowLimit = sol-err; highLimit = sol+err;

volání findzeros s nižším rozsahem vyhledávání. Pokud findzeros vrátí nuly, zkopírujte hodnoty do pole řešení a třídte je.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end

Call findzeros s vyšším rozsahem vyhledávání., Pokud findzeros vrátí nuly, zkopírujte hodnoty do pole řešení a třídte je.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend

celá funkce findzeros je následující. Uložte tuto funkci jako findzeros.m do aktuální složky.

syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'

Získat Řešení s Libovolnou Přesností

Použití digits nastavit přesnost řešení vrácené vpasolve., Ve výchozím nastavenívpasolve vrací řešení s přesností 32 významných čísel.

f = exp(x/7)*cos(2*x);vpasolve(f)

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

Použití digits zvýšit přesnost 64 významných osobností. Při úpravě digits se ujistěte, že uložíte jeho aktuální hodnotu, abyste ji mohli obnovit.,

digitsOld = digits;digits(64)vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')

Next, změnit přesnost řešení na 16 platných číslic.

digits(16)

Řešit Vícerozměrné Rovnice Pomocí Vyhledávání Rozpětí

Zvažte následující systém rovnic.

graf rovnice pro 0≤x≤2,5 a 0≤x≤2.5 ukazuje, že tři plochy se protínají ve dvou bodech., Pro lepší vizualizaci grafu použijte view. Pro měřítko hodnot colormap použijte caxis.

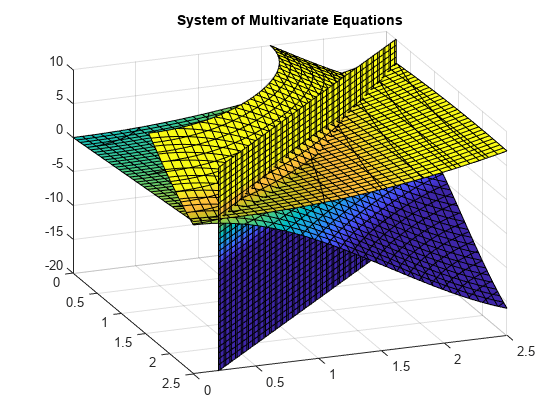
použijte vpasolve k nalezení místa, kde se povrchy protínají. Funkce vpasolve vrací strukturu. Pro přístup do x-, y – z-hodnoty roztoku, index do struktury.,

sol = vpasolve(equations);

hledat oblasti řešení prostoru, zadejte vyhledávací rozsahy proměnných. Pokud zadáte rozsahy 0≤x≤1.5 a 1.5≤y≤2.5, pak funkce vpasolve vyhledá ohraničenou oblast.

Použití vpasolve najít řešení pro tento rozsah hledání. Chcete-li vynechat rozsah vyhledávání pro z, nastavte třetí rozsah vyhledávání na .,

vars = ;range = ;sol = vpasolve(equations, vars, range);

najít více řešení, nastavte 'Random' možnost true. Díky tomu vpasolve používají náhodné výchozí body při následných jízdách. 'Random' volba může být použita ve spojení s vyhledávací rozsahy vpasolve použít náhodné východiska v rámci vyhledávacího rozsahu. Protože 'Random' vybírá výchozí body náhodně, stejné řešení lze nalézt při následných hovorech., Zavolejte vpasolve opakovaně, abyste zajistili, že najdete obě řešení.

vykreslete rovnice. Řešení překrývají jako rozptyl bodů se žlutými značkami X pomocí scatter3. Chcete-li lépe vizualizovat spiknutí, vytvořte dva povrchy průhledné pomocí alpha. Měřítko mapy se děj hodnoty pomocí caxis, a změnit perspektivu pomocí view.

vpasolve najde řešení na průsečíku povrchů vytvořených rovnicemi, jak je znázorněno.,

Lastly, restore the old value of digits for further calculations.

digits(digitsOld)