začněme přímočarým příkladem, řekněme, že chceme vynásobit (2x-3)3. To nebude příliš obtížné dělat dlouhé ruce, ale pojďme použít binomickou větu tak, že když narazíte na větší expanze jako dvojčleny zvýšil na 4, 5, 6, … schopnosti budete přesně vědět, co dělat.
Chcete-li začít, musíte identifikovat dva pojmy z binomického (X a Y pozice našeho vzorce výše) a moc (n)rozšiřujete binomický na.,
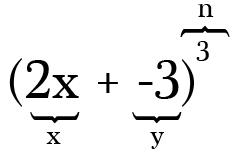
například, rozšířit (2x-3)3, tyto dva pojmy jsou 2x a -3 a sílu, nebo n hodnota je 3. Všimněte si, že vždy, když máte odčítání v binomické je to oh tak důležité mít na paměti, aby zahrnovala minus jako negativní symbol na doprovodný termín.
úžasná věc o binomickou větu, je to nám umožňuje najít rozšířené polynom bez vynásobením banda dvojčleny spolu. Docela hezké, že?, Ukazuje se, že počet termínů ve vašem rozšířeném polynomu bude vždy o jeden více než síla, kterou rozšiřujete. To znamená, že budeme vytvářet polynom se 4 termíny, protože síla v tomto příkladu je 3.
každý termín bude mít (2x) a (-3), stejně jako vzorec „n zvolte k“, kde n=3. Můžete pokračovat a zapsat to 4 krát, jeden pro každý termín, takže hodnota k v „n vybrat k“ a pravomoci prázdné pro tuto chvíli.
Dále budete chtít vyplnit hodnoty a síly k. Zde můžete sledovat vzorec součtu a zvýšit sílu pro každý termín., Ale je docela snadné sledovat vzory.
hodnoty k v „n zvolte k“, začne k=0 a zvýší se o 1 v každém termínu. Poslední termín by měl skončit n rovným k, v tomto případě n=3 a k=3.
dále musíme přidat síly na (2x) a (-3).
zapnutí (2x) začne hodnotou n, takže v tomto případě 3 a sníží se o 1 na každém termínu, dokud se nedostanete na nulu. Zapnutí (-3) začne nulou a pokaždé se zvýší o jednu, dokud se v tomto problému nedostanete na n nebo 3.,

Protože každá hodnota zvýšila na nultou se rovná 1, můžete zjednodušit výrazy s mocninami nuly.

Další jít dopředu a vztahují se pravomoci a zjednodušit kdekoli je to možné.,

pascalův Trojúhelník Zkratky

poslední část je řešit kombinací vzorce. Zřejmým způsobem, jak toho dosáhnout, je použít vzorec kombinací pro každý problém. Ale uděláme tu pěknou zkratku pomocí Pascalova trojúhelníku.
Pascalův trojúhelník je jednoduchý, ale silný trojúhelník tvořený vytvořením trojúhelníku se třemi 1., Pro každý řádek poté stačí napsat 1 je na obou koncích, a najít prostřední číslo (y) přidáním dvě hodnoty přímo nad ním.

tady je ta dobrá část. Skryté v Pascalově trojúhelníku jsou všechny odpovědi na jakékoli „n vybrat k“! Je to jako tajný malý podvodník!
níže uvedený diagram ukazuje, kde se nachází skryté „n zvolte k“.,

Pro náš problém potřebujeme řešit: 3 zvolte 0, 3 vybrat 1, 3 vybrat 2 a 3 vyberte 3. Což jsou všechny hodnoty ve 4. řádku. Takže vše, co musíme udělat, je podívat se na 4.řádek Pascalova trojúhelníku a porovnat odpovědi.
4. řádek má hodnoty: 1, 3, 3, 1. Takže budu jen nahradit odpovědi na naše n vybrat k.,

a Konečně, vše, co musíte udělat, je násobit a zjednodušit každý termín, to je nejjednodušší formě. Nezapomeňte zkontrolovat svou konečnou odpověď, abyste se ujistili, že pravomoci v každém termínu stále zvyšují míru původního binomického! Věř mi, je to neuvěřitelně snadné, aby se chyby v přepisu na tento typ problému 😉
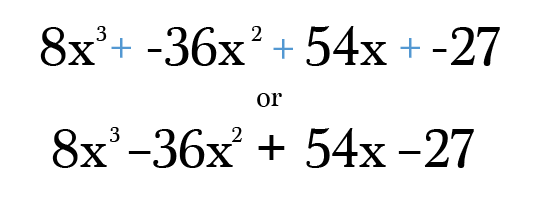
Potřebujete další příklad?,
ve výše uvedeném videu vám ukážu, jak použít binomickou větu k rozšíření binomického (x – 3y)⁵. Navíc vám ukážu několik dalších triků, jak zůstat organizovaný, a pár rychlých kontrol, které můžete použít k snadné identifikaci běžných chyb.
Díky za čtení!
❤ Zůstaňte ve spojení ❤
Zůstaňte v obraze se vším, co matematické hacky dělají!