
Diracova delta funkce je funkce zavedena v roce 1930 P. a. M. Dirac ve své podnětné knize o kvantové mechanice. Fyzikální model, který vizualizuje funkci delta, je hmotnostní rozdělení konečné celkové hmotnosti M-integrál nad hmotnostní distribucí., Při rozdělení se stává menší a menší, zatímco M je konstantní, hmotnostní distribuční zmenší na hmotný bod, který má, podle definice, nula rozsahu, a přesto má konečný-oceňují integrál roven celkové hmotnosti M. V limitu hmotný bod rozdělení se stává Diracova delta funkce.
Heuristicky, Diracova delta funkce může být viděn jako rozšíření Kroneckerovo delta z integrální indexy (prvky 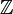 ), aby se skutečné indexy (prvky
), aby se skutečné indexy (prvky 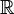 )., Všimněte si, že Kroneckerovo delta působí jako „filtr“ v součtu:
)., Všimněte si, že Kroneckerovo delta působí jako „filtr“ v součtu:
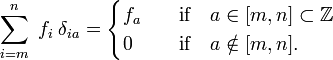
analogicky, Diracova delta funkce δ(x−a) je definován (nahradil jsem tím x a součtu více než jsem integrací přes x),
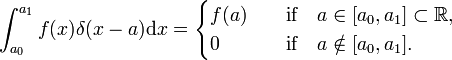
Diracova delta funkce není obyčejný dobře vychovaný mapa 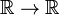 , ale rozdělení, známý také jako nepravý nebo zobecněné funkce. Fyzici vyjadřují svůj zvláštní charakter tím, že Diracova delta funkce má smysl pouze jako faktor integrovaná („pod nedílnou součástí“)., Matematici říkají, že funkce delta je lineární funkční v prostoru testovacích funkcí.
, ale rozdělení, známý také jako nepravý nebo zobecněné funkce. Fyzici vyjadřují svůj zvláštní charakter tím, že Diracova delta funkce má smysl pouze jako faktor integrovaná („pod nedílnou součástí“)., Matematici říkají, že funkce delta je lineární funkční v prostoru testovacích funkcí.
Obsah
- 1 Vlastnosti
- 2 Delta-konvergentní posloupnosti
- 2.1 Blokové funkce
- 2.2 Gaussova funkce
- 2.3 Lorentz-Cauchy funkce
- 2.4 Sinc funkce
- 3 Deriváty delta funkce
- 3.,1 Vlastnosti derivace
- 4 Primitivní
- 5 Diracova delta funkce ve třech dimenzích
- 6 Odkazy
Vlastnosti
Nejčastěji jeden má dolní a horní mez v definici delta funkce se rovná 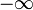 a
a 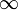 , resp. Odtud to bude hotovo.
, resp. Odtud to bude hotovo.
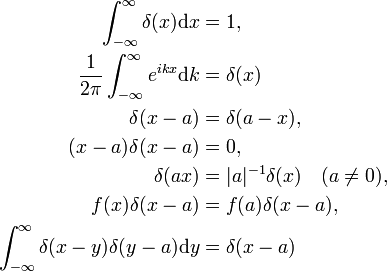
důkaz fyzika o těchto vlastnostech probíhá provedením správných substitucí do integrálu a použitím běžných pravidel integrálního počtu., Funkce delta jako Fourierova transformace funkce jednotky f (x) = 1 (druhá vlastnost) bude prokázána níže. Poslední vlastnost je analogie z násobení dvou matice identity,
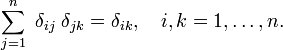
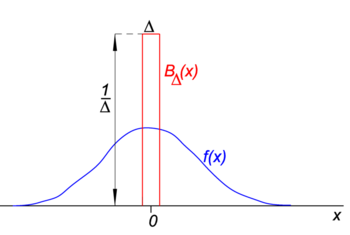
Obr. 1. Funkce bloku („boxcar“) (červená) krát běžná funkce f (x) (modrá).
Delta-konvergentní sekvence
existují rodiny pravidelných funkcí Fa (x), jejichž členové rodiny se liší hodnotou jediného parametru α., Příkladem takové rodiny je rodina Gaussovských funkcí Fa (x) = exp (−ax2), kde různé hodnoty jediného parametru α rozlišují různé členy. Když všichni členové jsou lineárně normalizable, tj. následující integrál je konečný, bez ohledu na to, α,
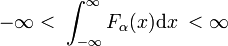
a všichni členové vrcholu kolem x = 0, pak rodina může tvořit delta-konvergentní posloupnost.,
blokové funkce
nejjednodušší příklad Delta-konvergentní sekvence je tvořen rodinou blokových funkcí, charakterizovaných pozitivním Δ,
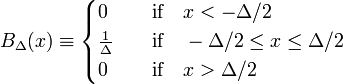
Na obr. 1 funkce bloku BΔ je zobrazena červeně. Je zřejmé, že plocha (šířka x výška) pod červenou křivkou je rovna jednoty, bez ohledu na hodnotu Δ,
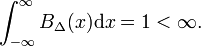
Ať je libovolná funkce f(x) (modře na Obr. 1) být kontinuální (žádné skoky) a konečný v sousedství x=0., Když Δ se stává velmi malé, a blokovat funkci velmi úzké (a nutně velmi vysoké, protože šířka krát výška je konstantní) produkt f(x) BΔ(x), se stává v dobrém přiblížení se rovná f(0) BΔ(x). Čím užší je blok, tím lepší je přiblížení., Tedy pro Δ jde k nule,
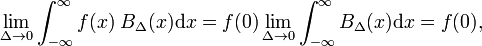
, které mohou být ve srovnání s definicí delta funkce,
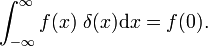
To ukazuje, že rodina bloku funkce konverguje k Diracova delta funkce pro snížení parametru Δ; rodina tvoří delta-konvergentní posloupnost:
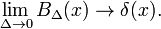
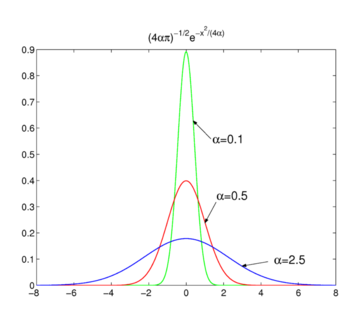
Obr. 2. Gaussovské funkce.
Poznámka: integrovali jsme se přes celou skutečnou osu., Samozřejmě to není nutné, mohli jsme vyloučit nulová křídla blokové funkce a integrovat pouze přes hrb uprostřed, od-Δ / 2 do + Δ / 2. V matematických textech, např. Ref. , toto zdokonalení v integračních limitech je zahrnuto do definice Delta-konvergentní sekvence. To znamená, že je nutné, aby integrály přes dvě křídla zmizely v limitu. Protože Delta-konvergentní sekvence, se kterými se setkáváme ve fyzických aplikacích, obvykle splňují tuto podmínku, vynecháme přesnější matematickou definici.,
Gaussovské funkce
zvažte rodinu,
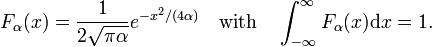
, jak je znázorněno na obr. 2 funkce vrcholí kolem x = 0 a zužují se pro snížení α. Proto rodina Gaussova funkce, formy delta-konvergentní posloupnost,
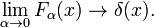
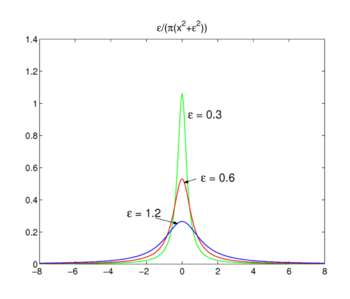
Obr. 3. Funkce Lorentz-Cauchy
funkce Lorentz-Cauchy
rodina funkcí zobrazených na obr., 3
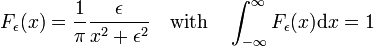
forms a delta-convergent sequence,
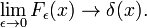
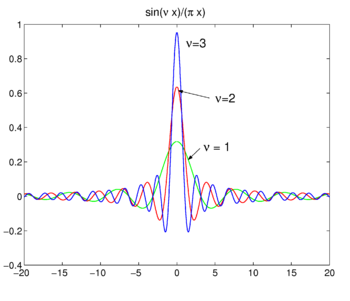
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 je
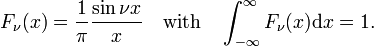
Tato rodina konverguje k delta funkce pro zvýšení ν
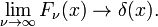
Tento limit vede snadno k Fourierova integrální reprezentace delta funkce:
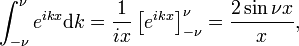
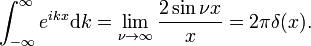
Diracova delta funkce je Fourierovou transformací jednotka funkce f(x) = 1.
deriváty funkce delta
zvažte diferencovatelnou funkci f (x), která zmizí v plusu a mínus nekonečno.,d=“ed7dae11d6″>
V stejným způsobem, jako jedna dokazuje obrat pravidlo a Hermiticity kvantové mechanické hybnosti operátor 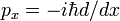 , ukázali jsme zde, že d/dx je anti-Hermitian,
, ukázali jsme zde, že d/dx je anti-Hermitian,
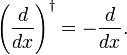
ve skutečnosti, když jsme se napsat integrál jako skalární součin, vyplývá z částečné integrace a mizející f(x) na integraci omezení, že
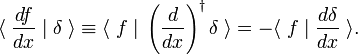
Tento obrat pravidlo se používá jako definice derivace delta funkce,
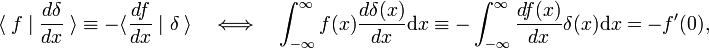
prime označuje první derivaci f(x)., Podle definice funkce delta je první derivát vyhodnocen v x = 0. Pomocí m krát obrat pravidlo, z toho vyplývá, že mth derivaci delta-funkce je definována
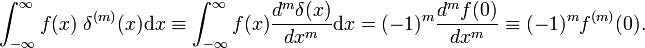
Vlastnosti derivace
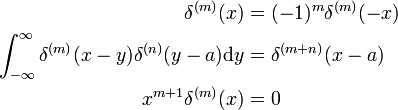
Tyto výsledky může být prokázáno tím, že substituci x → −x a použití obratu pravidlo pro d/dx (viz výše).,
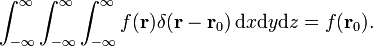
trojrozměrné delta funkce lze faktorizovat
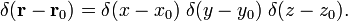
V sférické polární souřadnice,
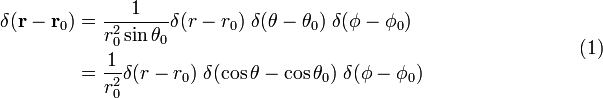
Důkaz rovnice (1)
Psát
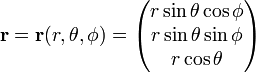
Jakobiho (Jacobiho determinant) této transformace z Kartézských souřadnic do sférických polárních souřadnicích,
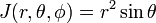
Za
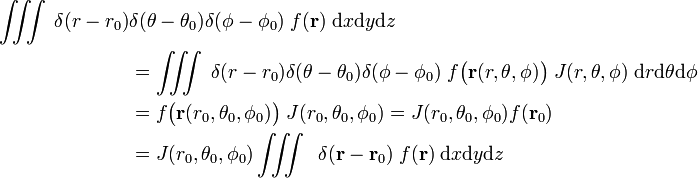
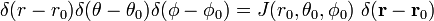
a
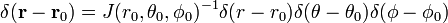
poslední řádek v rovnici (1) vyplývá z řetízkové pravidlo.,
následující užitečné a často použita vlastnost se ukázala jako tady,
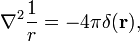
kde ∇2 je Laplaceův operátor v trojrozměrné Kartézské souřadnice a r je délky, r‘.