Logaritmické funkce jsou inverses exponenciální funkce. Inverzní exponenciální funkce y = ax je x = ay. Logaritmická funkce y = logax je definována jako ekvivalent exponenciální rovnice x = ay. y = logax pouze za následujících podmínek: x = ay, a > 0 a a≠1. Nazývá se logaritmická funkce se základnou a.
zvažte, co inverzní funkce Exponenciální znamená: x = ay., Vzhledem k tomu, číslo x a základ a, na jaký výkon y musí být zvýšena na rovno x? Tento neznámý exponent, y, se rovná logaxu. Takže vidíte, že logaritmus není nic jiného než exponent. Podle definice, alogax = x, pro každý skutečný X > 0.
Níže jsou na obrázku grafy tvaru y = logax, když > 1 a pokud 0 < < 1. Všimněte si, že doména se skládá pouze z pozitivních reálných čísel a že funkce se vždy zvyšuje s nárůstem x.,
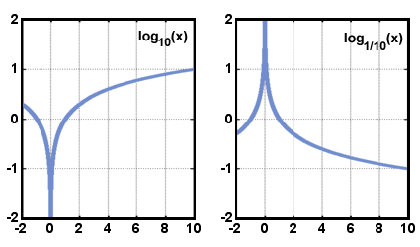
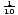 x.
x.doména logaritmické funkce je reálná čísla větší než nula, a rozsah je reálných čísel. Graf y = logax je symetrický k grafu y = ax vzhledem k řádku y = x. tento vztah platí pro jakoukoli funkci a její inverzní.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(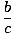 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
přírodní logaritmické funkce je logaritmická funkce o základu e. f (x) = log e = ln x, kde x > 0. ln x je jen nová forma notace pro logaritmy se základnou e. většina kalkulaček má tlačítka označená “ log “ a „ln“. Tlačítko “ log „předpokládá, že základna je deset a tlačítko“ ln “ samozřejmě umožňuje základnu rovnat e., Logaritmická funkce se základnou 10 se někdy nazývá společná logaritmická funkce. Používá se široce, protože náš číslovací systém má základnu ten. Přírodní logaritmy jsou vidět častěji v počtu.
existují dva vzorce, které umožňují změnu základny logaritmické funkce. První uvádí toto: logab = 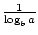 . Slavnější a užitečnější vzorec pro změnu základů se běžně nazývá změna základního vzorce. Umožňuje změnit základnu logaritmické funkce na libovolné kladné reálné číslo ≠1. Uvádí, že logax =
. Slavnější a užitečnější vzorec pro změnu základů se běžně nazývá změna základního vzorce. Umožňuje změnit základnu logaritmické funkce na libovolné kladné reálné číslo ≠1. Uvádí, že logax = 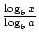 ., V tomto případě jsou A, b A x všechna kladná reálná čísla a A, B≠1.
., V tomto případě jsou A, b A x všechna kladná reálná čísla a A, B≠1.
v další části budeme diskutovat o některých aplikacích exponenciálních a logaritmických funkcí.