„Jednotková Kružnice“ je kruh s poloměrem 1.
být tak jednoduchý, je to skvělý způsob, jak se učit a mluvit o délkách a úhlech.
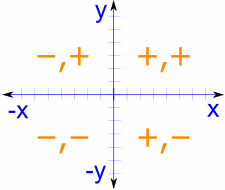
střed je umístěn na grafu, kde se kříží osa x a osa y, takže zde získáme toto úhledné uspořádání.
Sinus, Kosinus a Tangens
Protože poloměr je 1, můžeme přímo měřit sinus, cosinus a tangens.,
Co se stane, když úhel θ, je 0°?
cos 0° = 1, sin 0° = 0 a tg 0° = 0
Co se stane, když θ je 90°?
cos 90° = 0, sin 90° = 1 a tan 90° je nedefinováno
zkuste to sami!
Vyzkoušejte!, Pohybujte myší kolem, abyste zjistili, jak různé úhly (v radiánech nebo stupních) ovlivňují sinus, kosinus a tečnu
„strany“ mohou být podle pravidel kartézských souřadnic pozitivní nebo negativní. To také způsobuje změnu sinusu, kosinu a tangentu mezi pozitivními a zápornými hodnotami.
vyzkoušejte také interaktivní kruh jednotky.,
podle pythagorovy věty
pythagorova Věta říká, že pro pravoúhlý trojúhelník, čtverec dlouhé straně se rovná součtu čtverců ostatních dvou stran:
x2 + y2 = 12
Ale 12 je jen 1, takže:
x2 + y2 = 1
(rovnice jednotkové kružnice)
Také, protože x=cos a y=sin, dostaneme:
(cos(θ))2 + (sin(θ))2 = 1
užitečné „identita“
Důležité Úhly: 30°, 45° a 60°
měli Byste se pokusit vzpomenout sin, cos a tan pro úhly 30°, 45° a 60°.,
ano, ano, je to bolest, že si musíte pamatovat věci, ale usnadní vám to život, když je znáte, nejen při zkouškách, ale jindy, když potřebujete udělat rychlé odhady atd.
to jsou hodnoty, které byste si měli pamatovat!,id=“0f47f3223b“>
What about tan?,
No, tan = sin/cos, takže můžeme vypočítat takto:
tan(30°) =sin(30°), protože(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin(45°), protože(45°) = √2/2√2/2 = 1
tan(60°) =sin(60°), protože(60°) = √3/21/2 = √3
* Poznámka: psaní 1√3 mohou stát značky (viz Racionální Jmenovatele), tak místo toho použít √33
Rychlé Skici
Další způsob, jak pomoci si pamatujete 30° a 60° je udělat rychlou skicu:
| Nakreslit trojúhelník o straně délky 2 | 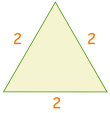 |
|
|
Snížit na polovinu.,div id=“56c966b492″> Příklad: sin(30°)Sinus: sohcahtoa sinus je protilehlá děleno přepona
sin(30°) = oppositehypotenuse = 12
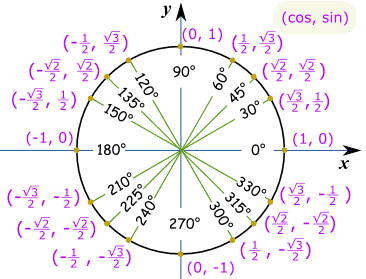
Celý KruhPro celý kruh potřebujeme hodnoty v každém kvadrantu, se správnou plus nebo mínus podle Kartézských Souřadnicích: Všimněte si, že protože je první a hřích je druhý, tak to jde (protože, hřích):
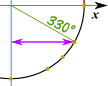
Uložit jako PDF Příklad: Co je cos(330°) ?,
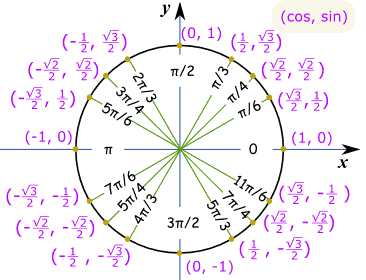
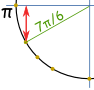
Udělat náčrt, jako je tento, a můžeme vidět, že je „dlouhá“ hodnota: √32 A to je stejné Jednotkové Kružnici v radiánech. příklad: co je hřích (7π/6) ?
Myslíš, že „7π/6 = π + π/6“, pak se náčrt. pak můžeme vidět, že je negativní a je“ krátká “ hodnota: – ½ |