Na těchto stránkách se podíváme na některé zajímavé koncepty, se podíváme na to, zakřivený prostor: to, co zakřivený prostor znamená, jak můžeme říct, když prostor je zakřivený zevnitř, nebo z venku.
podíváme se na to, jak můžeme vložit typ prostoru do jiného a uvidíme, že můžeme mapovat mezi různými mezerami různými způsoby.
podíváme se také na kompaktování a na to, jak můžeme v našich prostorech představovat nekonečně velké a nekonečně malé vektory způsobem, který nevede k singularitám a dalším problémům.,
tyto pojmy se ukáží jako užitečné, i když pracujeme s plochým prostorem, najdeme způsoby, jak reprezentovat vektory a roviny, které neprocházejí původem. To nám dává způsoby, jak reprezentovat rotace a překlady jako jednu operaci.
druhou aplikací je relativistický časoprostor.
Rienmannian Geometrie
V Rienmannian geometrie prostoru může křivka na různých místech (viz rozvody) zde se podíváme na to, geometrie, kde křivka prostoru je konstantní.,
Eulidean Geometrie
plochý prostor,
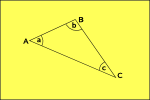
Hyperbolické Geometrii
prostor, křivky směrem ven,
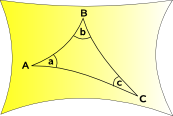
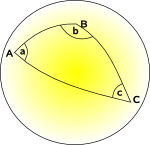
Sférické Geometrie a Eliptické Geometrii,
prostor, křivky dovnitř,
V zakřivené (Non-Euklidovský) geometrie nemůžeme najít souřadnice, které jsou vzájemně kolmé, kde souřadnicové čáry jsou rovnoběžné k sobě navzájem, a kde každý čtverec mřížky má stejné oblasti., Možná najdeme souřadnicový systém, kde můžeme udělat některé z nich, ale ne všechny.
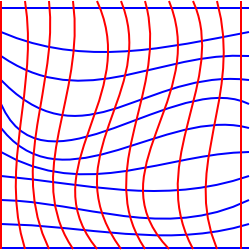
Tento diagram se snaží ilustrovat tuto situaci na 2 rozměry, i když je to trochu zavádějící, protože jsme nakreslili to na rovině, takže jsme mohli vyvodit pravoúhlé souřadnice.
abychom se pokusili ilustrovat situaci, kdy to není možné, mohli bychom myslet na dvourozměrnou rovinu, která byla natažena do třetí dimenze.,

V této situaci si můžeme vybrat souřadnice, které tvoří obdélníkové mřížky, když promítá na horizontální rovině, nicméně, osoby žijící v povrchu pak některé z čtverců mřížky se zdá, mají větší plochu než ostatní a čáry mřížky nemusí být paralelní. Neexistuje žádný dvourozměrný souřadnicový systém, který by zachoval paralelní linie, úhly a oblasti současně.,
podobný příklad se snaží mapovat povrch země, můžeme použít zeměpisné šířky a délky linek, ale délky linek přiblížit bližší pólům.
v těchto případech bychom mohli pracovat z hlediska 3 dimenzionálních souřadnic a to je přístup, který budeme mít s některými typy neeuklidovských geometrií. Často je možné vložit určitou geometrii do vyšší rozměrové geometrie, aby byla více euklidovská.,
někdy se stává, že když se podíváme na geometrii ve velkém měřítku, že je Neeuklidská, ale pokud se na ni podíváme v menším a menším měřítku, přibližuje se euklidovské geometrii. K tomu musíme najít souřadnicový systém, kde jsou úhly zachovány v každém bodě, to znamená, že vodorovné a svislé souřadné čáry musí vždy protínat při 90°, i když čáry nemusí být rovné. Toto je známé jako konformní geometrie. V tomto typu geometrie můžeme alespoň definovat lokální souřadnicový systém.,
souvisí s tím, zda lze geometrii diferencovat a integrovat, podmínkou je, že musí být dobře vychovaná a nesmí mít žádné náhlé skoky atd. Některé geometrie a souřadnicové systémy mohou být dobře choval v některých místech, ale mají singularity atd.
pro diskusi o tom, jak se měří zakřivení, viz tato stránka.
Matematická notace
Jak se vypořádáme s geometrií, kde nemůžeme použít všechna pravidla, která se vztahují na euklidovskou geometrii?,
jedním z přístupů je použití tenzorové notace, což poskytuje konvence a notaci, které nám pomáhají při přepínání mezi různými souřadnicovými systémy. Ortogonální souřadnicový systém, Lokální do libovolného bodu, lze definovat pomocí základních vektorů, které jsou tečny k souřadnicovým čarám.,Potrubí
tuto stránku
Vztah mezi Hyperbolické a Minkowského Geometrie
| Minkowského Geometrii | Hyperbolické Geometrie | |
| události v časoprostoru | částice rovnoměrný pohyb | |
| vzdálenost mezi těmito dvěma body | prostor-časový interval mezi dvěma událostmi | relativní rychlost mezi dvě takové částice |
Názvosloví
Tady se podíváme na terminologii jako geometrie, prostor, modely, projekce a transformace., Je to docela obtížné, když začneme řešit neeuklidovské geometrie, protože používáme podobnou terminologii, na kterou jsme zvyklí v konvenčním euklidovském prostoru, ale termíny mohou mít mírně odlišné vlastnosti.,zkusit
Elliptic Geometrie
Modely
Příklady jsou:
- Horní polovina-model letadla
- Poincarého disk model
- Projektivní model
- Konformní model
Projekce
Stereografická Projekce
Transformace
Invariantní
Příklady jsou:
- Möbius Transformovat
- Lorentzova Transformace
Paralelní Předpokládat
Pokud odstraníme paralelní předpokládat z Euklidovský Prostor.,
Toto vede k:
- paralelní postulát je false
- úhlů v trojúhelníku nepřispívají k π
- pro tvar dané velikosti, není obecně, existují podobné tvaru větší velikosti.,ctive
konformní (Poincaré disk ) rovné čáry – geodesics segmenty kruhy úhel, zachovat vnitřní úhly trojúhelníku, π-(α+β+γ)=CΔ vzdálenost mezi těmito dvěma body