Konečné automaty mohou mít výstupy odpovídající jednotlivým přechod. Existují dva typy konečných stavových automatů, které generují výstup −
- Mealyho Stroj
- Moore stroj
Mealyho Stroj
Mealyho Stroj je FSM, jejichž výstup závisí na současném stavu, stejně jako současný vstup.,
to může být popsáno pomocí 6 Tice (Q, ∑, o, δ, X, q0), kde −
-
Q je konečná sada stavů.
-
∑ je konečná sada symbolů nazývaná vstupní abeceda.
-
O je konečná sada symbolů nazývaná výstupní abeceda.
-
δ je vstup přechodové funkce, kde δ: Q × Σ → Q
-
X je výstupní přechodové funkce, kde X: Q × Σ → O
-
q0 je počáteční stav, kde žádné zadání, je zpracována (q0 ∈ Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
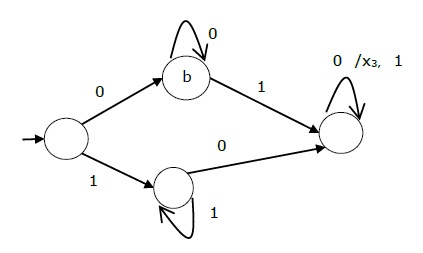
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
Mooreův stroj lze popsat pomocí 6 Tice (Q, ∑, O, δ, X, q0), kde −
-
Q je konečná sada stavů.
-
∑ je konečná sada symbolů nazývaná vstupní abeceda.
-
O je konečná sada symbolů nazývaná výstupní abeceda.
-
δ je vstup přechodové funkce, kde δ: Q × Σ → Q
-
X je výstupní přechodové funkce, kde X: Q → O
-
q0 je počáteční stav, kde žádné zadání, je zpracována (q0 ∈ Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
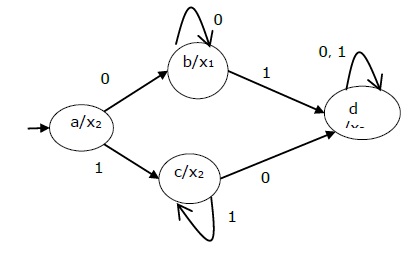
Mealy Machine vs., Moore Machine
následující tabulka zdůrazňuje body, které odlišují Mealy stroj od Moore stroje.
Mealyho Stroj Moore Stroj Výstup závisí jak na současný stav a současnou vstup Výstup závisí pouze na současném stavu. obecně má méně stavů než Moore Machine. obecně má více stavů než Mealy stroj., hodnota výstupní funkce je funkce přechodů a změn, když je provedena logika vstupu v současném stavu. hodnota výstupní funkce je funkcí aktuálního stavu a změn na okrajích hodin, kdykoli dojde ke změnám stavu. Mealy stroje reagují rychleji na vstupy. Obvykle reagují ve stejném hodinovém cyklu. ve strojích Moore je zapotřebí více logiky pro dekódování výstupů, což má za následek větší zpoždění obvodu. Obvykle reagují o jeden hodinový cyklus později., Moore Stroj Mealyho Stroje
Algoritmus 4
Input − Moore Stroj
Výstup − Mealyho Stroj,
Krok 1 − Take prázdné Mealyho Stroj přechodu formát tabulky.
Krok 2-Zkopírujte všechny stavy přechodu Moore Machine do tohoto formátu tabulky.
Krok 3-Zkontrolujte současné stavy a jejich odpovídající výstupy v tabulce stavu stroje Moore; pokud je pro výstup stavu Qi m, zkopírujte jej do výstupních sloupců tabulky stavu Mealy Machine, kdekoli se Qi objeví v dalším stavu.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
Krok 2-pokud jsou všechny výstupy Qi stejné, zkopírujte stav Qi. Pokud má n odlišné výstupy, rozbít Qi do n stavy jako Qin, kde n = 0, 1, 2…….
Krok 3-pokud je výstup počátečního stavu 1, vložte na začátek nový počáteční stav, který dává 0 výstup.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Státy “ b “ A “ c “ však produkují různé výstupy (1 a 0). Takže rozdělíme b na b0, b1 A c na c0, c1.,“>
Output