Obsah – Konstantní zrychlení

Obsah

Konstantní zrychlení.

všichni Jsme obeznámeni s faktem, že auto zrychlí, když jsme se dupnout na plyn. Rychlost změny rychlosti částice vzhledem k času se nazývá její zrychlení. Pokud se rychlost částice mění konstantní rychlostí, pak se tato rychlost nazývá konstantní zrychlení.,

například, pokud je rychlost částice pohybující se v přímce mění rovnoměrně (konstantní rychlostí změny) od 2 m/s 5 m/s přes jednu sekundu, pak jeho konstantní zrychlení je 3 m/s\(^2\).

Snížení rychlosti

Pokud se částice má počáteční rychlost 6 m/s a konstantní zrychlení \(-2\) m/s\(^2\), pak:

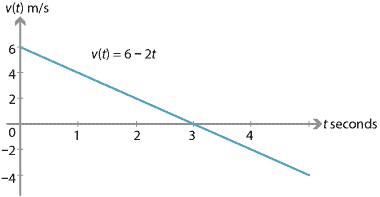
v Průběhu prvních tří sekund, částice je rychlost klesá (částice se zpomaluje). Po třech sekundách je částice momentálně v klidu., Po třech sekundách se rychlost stále snižuje, ale rychlost se zvyšuje (částice jde rychleji a rychleji).

Přehled

Pokud budeme předpokládat, že rychlost změny rychlosti (zrychlení) je konstantní, pak konstantní zrychlení je dané

\

přesněji řečeno, konstantní zrychlení \(a\) je dán vzorcem

\

, kde \(v(t_i)\) je rychlost v čase \(t_i\). Protože rychlost je vektor, tak je zrychlení.,

vzorce konstantního zrychlení pro pohyb v přímce

v této sekci uvažujeme o pohybu v přímce s konstantním zrychlením. Tato situace je velmi častá; například tělo pohybující se pod vlivem gravitace cestuje s konstantním zrychlením.

předpokládá se, že pohyb začíná, když \(t = 0\), a že počáteční pozice je považována za původ, to znamená \(x(0) = 0\).,

pět pohybové rovnice

1. \(v = u + v\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}at^2\)
4. \(v^2 = u^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}at^2\)

Poznámka:. Každá z pěti rovnic zahrnuje čtyři z pěti proměnných \(u, v, x, a, t\). Pokud jsou známy hodnoty tří proměnných, zbývající hodnoty lze nalézt pomocí dvou rovnic.,

Odvození konstantní zrychlení vzorce

první rovnice pohybu

Protože zrychlení je konstantní, máme \(a = \dfrac{v, u} a{t}\). To dává první rovnici pohybu, \(v = U + at\).

druhá pohybová rovnice

druhá rovnice,

\

říká, že posunutí se získá vynásobením průměr počáteční a konečné rychlosti podle času, který uplynul během pohybu. Jednodušeji:

\

tuto rovnici můžeme odvodit pomocí skutečnosti, že posun se rovná podepsané oblasti pod grafem rychlosti a času.,

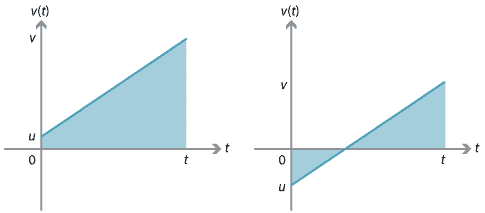
pro graf vpravo lze posun najít zvážením dvou trojúhelníků mezi grafem a osou\(t\). Jeden z trojúhelníků má pozitivní podepsanou oblast a druhý má negativní podepsanou oblast.

nalezení posunutí částice z grafu rychlosti a času pomocí integrace bude popsáno v pozdější části tohoto modulu.,

třetí rovnice pohybu

Nahradit za \(v\) z první rovnice do druhé rovnice dává

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+v)t}{2} \\ &= \dfrac{2ut+v^2}{2} \\ &= ut + \dfrac{1}{2}at^2, \end{align*}

což je třetí rovnice. Takže \(x\) je kvadratický v \(t\), a proto graf \(x\) proti \(t\) je parabola.

čtvrtá rovnice pohybu

Z první rovnice, máme \(t = \dfrac{v, u}{a}\)., Dosazením do druhé rovnice dává

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2, u^2}{2a}. \end{align*}

přeskupení tak, aby\ (v^2\) subjekt vytvořil čtvrtou rovnici: \ (v^2 = u^2 + 2AX\).

pátá rovnice pohybu

z první rovnice máme \(u = v-at\)., Pomocí druhé rovnice, dostaneme

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-v+v)t}{2} \\ &= \dfrac{2vt-v^2}{2} \\ &= vt-\dfrac{1}{2}at^2, \end{align*}

, která je pátou rovnici.

vertikální pohyb

pohyb způsobený gravitací je dobrým kontextem, ve kterém lze prokázat použití vzorců s konstantním zrychlením., Jak již bylo řečeno, naše dva směry ve vertikálním pohybu jsou nahoru a dolů a je třeba rozhodnout, který ze dvou směrů je pozitivní. Zrychlení v důsledku gravitace je konstantní, s magnitudou označenou \(g\). V následujícím příkladu vezmeme směr nahoru, aby byl pozitivní, a vezmeme \(g = 10\) m/s\(^2\).

Další použití pohybové rovnice

Next page – Content – Average velocity and average speed