průřezy

vlastnosti ploch

Centroid

centroid tvaru představuje bod, o kterém je oblast průřezu rovnoměrně rozložena. Pokud je oblast dvakrát symetrická asi dvěma ortogonálními osami, střed leží na průsečíku těchto OS. Pokud je oblast symetrická pouze o jedné ose, pak střed leží někde podél této osy (bude třeba vypočítat druhou souřadnici)., Pokud přesné umístění těžiště nemůže být určena tím, že kontroly, může být vypočten podle:

kde se dA představuje oblast nekonečně malý element, je celková plocha průřezu, a x a y jsou souřadnice elementu dA s ohledem na osy zájmu.,

středová místa společných průřezů jsou dobře zdokumentována, takže obvykle není nutné vypočítat umístění s výše uvedenými rovnicemi., základní tvary, jejichž těžištní místech je známo, že s ohledem na některé referenční bod, pak se těžiště umístění kompozitního průřezu lze vypočítat jako:

kde xc,i, yc,i, jsou pravoúhlé souřadnice těžiště, umístění i-tého oddílu s ohledem na referenční bod, a Ai je plocha i-té sekce.,

Těžištní Vzdálenost

těžiště, vzdálenost, c, je vzdálenost od těžiště průřezu k extrémní vlákno., Těžištní vzdálenost ve směru y pro obdélníkový průřez je zobrazen na obrázku níže:

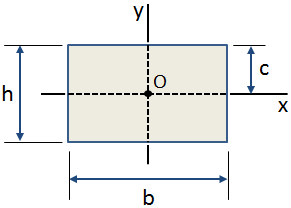
nejčastější použití pro těžištní vzdálenost zahrnovat:

• výpočet maximální ohybové napětí v průřezu
• výpočet hodnoty první okamžik oblasti, Q, výše bodu v průřezu k určení smykového napětí v tomto bodě

První Chvíle, kdy z Oblasti

první okamžik oblasti s ohledem na osu úrok se vypočítá jako:

Qx = ∫ y dA

Qy = ∫ x dA

kde Qx je první moment okolo osy x a Qy je první moment okolo osy y.,Je-li oblast je složena z kolekce základních tvarů, jejichž těžištní místech je známo, že s ohledem na osy zájem, pak první chvíli kompozitní oblasti může být vypočtena jako:

Všimněte si, že první okamžik oblast se používá při výpočtu těžiště průřezu s ohledem na některé původu (jak je popsáno dříve)., První okamžik se také používá při výpočtu hodnoty smykového napětí v určitém bodě průřezu. V tomto případě se první okamžik vypočítá pro oblast, která tvoří menší část průřezu, kde je oblast ohraničena bodem zájmu a extrémním vláknem (horní nebo dolní) průřezu. První okamžik se vypočítá o ose, která prochází středem průřezu.,

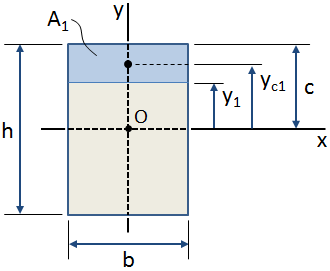
na obrázku výše, stínované modré oblasti je oblast zájmu v rámci celkového průřezu.,nt z této oblasti s ohledem na osy x (který prochází průřezem těžiště, bod O na obrázku výše) se vypočítá jako:

Pokud těžištní umístění oblastí zájmu je známo, pak první moment plochy k ose lze vypočítat jako (viz obrázek výše):

Je třeba poznamenat, že první okamžik oblasti bude pozitivní nebo negativní v závislosti na poloze poloha oblasti s ohledem na osy zájmu., Proto bude první okamžik celé plochy průřezu vzhledem k vlastnímu centroidu nulový.

Oblast Moment Setrvačnosti

druhý moment plochy, více obyčejně známý jako moment setrvačnosti, I průřez, je údaj o konstrukční prvek, je schopnost odolávat ohýbání.,(Poznámka 1) Ix a Iy jsou momenty setrvačnosti okolo x – a y – osy, respektive, a jsou vypočteny tím, že:

Ix = ∫ y 2 dA

Iy = ∫ x2 dA

kde x a y jsou souřadnice elementu dA s ohledem na osy zájmu.

nejčastěji se momenty setrvačnosti počítají s ohledem na centroid sekce. V tomto případě jsou označovány jako těžiště, momenty setrvačnosti a jsou označeny jako Icx pro setrvačnosti okolo osy x a Náledí na setrvačnosti kolem osy y.,

momenty setrvačnosti společných průřezů jsou dobře zdokumentovány, takže obvykle není nutné je vypočítat pomocí výše uvedených rovnic. Vlastnosti několika společných průřezů jsou uvedeny na konci této stránky.

Pokud se průřez skládá z kolekce základních tvarů, jejichž centroidy jsou všechny shodné, pak moment setrvačnosti složeného část je jednoduše součet jednotlivých momentů setrvačnosti. Příkladem je boxový paprsek, který se skládá ze dvou obdélníkových částí, jak je znázorněno níže., V tomto případě, vnější část má „pozitivní oblasti“ a vnitřní část má „negativní prostor“, takže kompozitní moment setrvačnosti je odčítání moment setrvačnosti vnitřní část z vnější části.

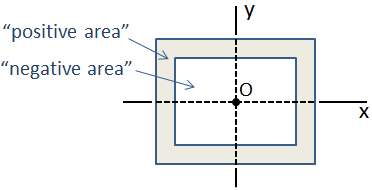
V případě složitější kompozitní průřez, ve kterém těžištní místech nejsou sjednocené, moment setrvačnosti lze vypočítat pomocí steinerova věta.

je důležité nezaměňovat moment setrvačnosti oblasti s hmotnostním momentem setrvačnosti pevného tělesa., Moment setrvačnosti ukazuje odolnost průřezu vůči ohybu, zatímco hmotnostní moment setrvačnosti označuje odpor těla vůči otáčení.,

steinerova Věta

Pokud moment setrvačnosti průřezu o k těžištní osa je známo, pak steinerova věta může být použit pro výpočet momentu setrvačnosti libovolné rovnoběžné ose:

kde Ic je moment setrvačnosti k těžištní ose, d je vzdálenost mezi těžištní ose a paralelní osy, a je plocha průřezu.,

Pokud se průřez skládá z kolekce základních tvarů, jejichž těžiště, momenty setrvačnosti jsou známé spolu se vzdáleností těžišť na nějaký referenční bod, pak steinerova věta může být použit pro výpočet momentu setrvačnosti složeného průřezu.

například I-paprsek může být aproximován 3 obdélníky, jak je znázorněno níže. Protože tento kombinovaný oddíl je symetrický na obě x – a y – osy, těžiště části mohou být umístěny podle inspekce v průsečíku těchto os. Centroid se nachází na počátku, O, na obrázku.,

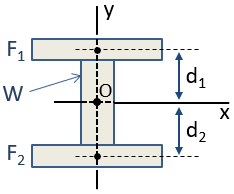
moment setrvačnosti složeného oddílu lze vypočítat pomocí steinerova věta. Středový moment setrvačnosti sekce kolem osy X, Icx, se vypočítá jako:

kde Icx podmínky jsou momenty setrvačnosti jednotlivých sekcí o jejich vlastní centroidy v orientaci osy x, d podmínek jsou vzdálenosti jednotlivých části centroidy pro kompozitní bod těžiště, a podmínky jsou oblasti jednotlivých sekcí. Protože centroid sekce W a centroid kompozitní sekce jsou shodné, d je pro tento úsek nulový, takže neexistuje termín Ad2.,

je důležité si uvědomit důsledky steinerova věta, že jako jednotlivec bod se pohybuje dále od těžiště složeného průřezu, příspěvek, že sekce kompozitní sekce je moment setrvačnosti zvyšuje o faktor d2. Pokud je tedy záměrem zvýšit moment setrvačnosti úseku o určité ose, je nejúčinnější lokalizovat oblast co nejdále od této osy. To vysvětluje tvar I-paprsku., Příruby jsou primárními přispěvateli momentu setrvačnosti a pás slouží k oddělení přírub od osy ohybu. Web však musí udržovat určitou tloušťku, aby se zabránilo vzpěru, a protože web v sekci zaujímá významnou část smykového stresu.

Polární Moment Setrvačnosti

polární moment setrvačnosti I průřezu je údaj o konstrukční prvek, je schopnost odolávat torzní kolem osy kolmé k průřezu., Polární moment setrvačnosti pro bod s ohledem na osy lze vypočítat podle:

kde x a y jsou souřadnice elementu dA s ohledem na osy zájem, a r je vzdálenost mezi elementem dA a osou zájmu.,

i když polární moment setrvačnosti lze vypočítat pomocí výše uvedené rovnice, je obvykle výhodnější vypočítat pomocí kolmé osy věta, která uvádí, že polární moment setrvačnosti plochy je součtem momentů setrvačnosti o nějaké dvě ortogonální osy, které procházejí osou zájmu:

Nejčastěji, osa zájem prochází těžištěm průřezu.,

Sekce Modul

maximální ohybové napětí v nosníku se vypočte jako σb = Mc / Ic, kde c je vzdálenost od neutrální osy krajní vlákno, Icis těžiště, moment setrvačnosti, a M je ohybový moment. Sekce modul v sobě spojuje c a Ic podmínek v ohybu rovnice:

Pomocí průřezový modul, napětí v ohybu se vypočítá jako σb = M / S. utility části modulu je, že to charakterizuje odolnost v ohybu průřezu v jeden termín., To umožňuje optimalizaci průřezu paprsku odolávat ohýbání maximalizací jediného parametru.

poloměr Gyrace

poloměr gyrace představuje vzdálenost od těžiště sekce, ve které by mohla být celá oblast soustředěna, aniž by to mělo vliv na moment setrvačnosti.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

Vlastnosti Běžných průřezů

uvedená tabulka obsahuje vlastnosti společné průřezy. Rozsáhlejší tabulky naleznete v uvedených odkazech.

vlastnosti vypočtené v tabulce zahrnují oblasti, těžiště, moment setrvačnosti, průřezový modul, a poloměr otáčení.,