
přemýšleli jste někdy, jak je sníh při teplotách nad bodem mrazu? Naivní vysvětlení je, že stačí, aby se sněhové vločky roztavily, jakmile proniknou nad mrazivý vzduch, když sestupují dolů k zemi. To je samozřejmě důvod, proč krupobití může spadnout za teplého počasí. Jednoduše, krupobití kameny padají rychle, příliš rychle, aby teplý vzduch roztavil krupobití. To však není hlavní vysvětlení, proč může sněžit, když je nad bodem mrazu.,
z obrázku níže je zřejmé, že existuje jasná závislost na vlhkosti – čím je sušší, tím teplejší může být při sněžení. To znamená, že hlavní faktor, alespoň v suchých podmínkách, má co do činění s vlhkostí. A tento faktor je odpařování. Konkrétněji, jak sněhové vločky sestupují, odpařují se. Tento proces trvá teplo a udržuje vločky chladné.
Pokud tedy chceme vypočítat maximální teplotu, musíme odhadnout čistou tepelnou rovnováhu vloček. Za prvé, jak vločky cestují v teplém prostředí, získávají teplo z okolí prostřednictvím vedení., Za druhé, teplo se používá k odpařování vloček, čímž je ochlazuje. Pokud je odpařovací chladič větší než vedení tepla, vločky zůstanou zmrazené.
ukazuje se, že to lze snadno vypočítat. Ne, není jednoduché vypočítat vedení tepla nebo odpařovací teplo, ale poměr je, protože různé neznámé geometrické faktory se vyruší.
Pokud se nestaráte o výpočet (protože nejste vědcem), můžete jednoduše navštívit stránku kalkulačky.
Pokud vám záleží, zde je odvození., Předpokládejme, že tok kolem vloček je takový, že se kolem něj vytvoří hraniční vrstva šířky d. Celkový tepelný tok $F_H$ vločka (např., J/sec v MKS) bude mít podle Fourierova zákona:
kde $\kappa$ je teplo difúzní koeficient ve vzduchu (např. m2/sec v MKS), c je tepelná kapacita vzduchu (J/kg v MKS), A je plocha povrchu mezní vrstvy kolem flaku, zatímco ΔT je teplotní rozdíl mezi vločka a prostředí.,
Podobně, jeden může používat fickova zákona pro získání difúze vodních par z vloček (kde je teplota v blízkosti zmrazení, a relativní vlhkost vzduchu je 100%), do okolního prostředí, kde je vyšší teplota a relativní vlhkost vzduchu nižší:
zde je D koeficient difúze vody (např. m2/s v MKS) a ρ je hustota vodní páry (kg/m3 v MKS).,
vypařování ledu vyžaduje teplo, takže, pokud tam je vodní pára hmotnostní tok Φ z vloček, to by vyžadovalo tepla ve výši $F_w = \epsilon \Phi$, kde $\epsilon$ je teplo odpařování ledu (J/kg v MKS).
nejvyšší teplota, nad kterou vločka taje, je teplota, za které dva tepelné toky jsou rovné:
Všimněte si, že geometrie toku kolem vloček se zruší, protože oba tepelné toky závisí na d A a stejným způsobem., To by bylo také v případě, že hraniční vrstva kolem vloček je složitá tak, že d skutečně závisí na směru. Proto
kde$ \ rho_{sat} $ je hustota nasycení vodní páry.
zapojení čísel (které lze nalézt například v příručce chemie a fyziky CRC), výsledky s implicitní rovnicí pro teplotuprotože hustota nasycení vodní páry závisí také na teplotě., Můžeme věci zjednodušit, když se místo toho ptát, jaká je relativní vlhkost vzduchu potřebné k udržení vločka, zmrazené při dané teplotě. To je:
kde $t_c$ je teplota ve stupních Celsia.
tuto funkci lze vidět na obrázku níže, spolu s daty z Matsuo a Sasyo, 1981. Jak je vidět z obrázku, vypočítaný graf je zhruba dolní mez, pod kterou není vůbec žádný déšť. Při teplejších teplotách je směs., Až kolem 1°C nad čarou tání je většinou sníh, zatímco mezi 1°C a 2 ° C nad čárou je většinou déšť, ale sníh je možný. Tyto události mohou být způsobeny dalšími účinky,jako jsou silné downdrafty, čas potřebný k roztavení sněhu atd.
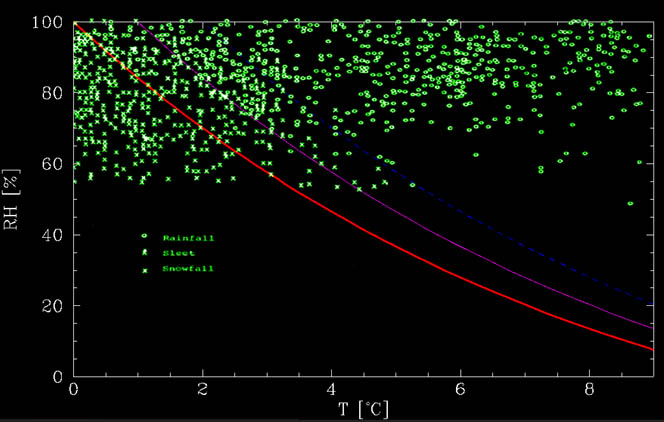
pokud tedy chceme pozorovat teplé počasí, jsou vyžadovány velmi suché podmínky. Například, pokud je vlhkost půdy pouze asi 20% (velmi vzácné, protože pokud dojde k srážení, atmosféra je obecně mokrá!) pak by mohlo sněžit při 8°C (nebo 46°F pro anglické uživatele).,
dalším požadavkem je, že nikde podél sestupu nepřekračuje vzduch linii taveniny. Pokud ano, vločka se samozřejmě roztaví.
pokud teplota stoupne nad bod mrazu, neexistují žádné parametry, s nimiž lze určit typ srážek pro jistotu. Vše, co pak můžeme předvídat, je pravděpodobnost, že sníh skutečně padne. To lze provést pomocí výsledků Häggmark a Ivarsson (1997), pouze opravené pro použití zmrazené žárovky a nikoli teploty mokré žárovky.
pointa je kalkulačka, pomocí které lze odhadnout pravděpodobnost sněhu.,