lad os begynde med et ligetil eksempel, siger vi vil multiplicere ud (2.-3)3. Dette ville ikke være for svært at gøre lang hånd, men lad os bruge binomial sætningen, så når du støder på større udvidelser som binomials hævet til 4, 5, 6, … beføjelser, ved du præcis, hvad du skal gøre.
for at komme i gang skal du identificere de to udtryk fra din binomial (positions-og y-positionerne i vores formel ovenfor) og kraften (n), du udvider binomialen til.,
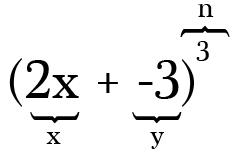
For eksempel, at udvide (2x-3)3, de to begreber er 2x og -3 og magt, eller n-værdi, er 3. Bemærk, at når du har en subtraktion i din binomial, er det åh så vigtigt at huske at inkludere minus som et negativt symbol på det ledsagende udtryk.
den vidunderlige ting ved binomial-sætningen er, at det giver os mulighed for at finde det udvidede polynom uden at multiplicere en flok binomialer sammen. Ret pænt, ikke?, Det viser sig, at antallet af udtryk i dit udvidede polynom altid vil være en mere end den magt, du udvider. Det betyder, at vi opretter et polynom med 4 udtryk, da strømmen i dette eksempel er 3.
hvert udtryk vil have en (2 and) og (-3) samt formlen “N vælg k”, hvor n=3. Du kan gå videre og skrive det ned 4 gange, en for hver periode, forlader k-værdien i “n vælg k” og kræfterne er tomme for øjeblikket.
næste vil du udfylde k-værdier og beføjelser. Her kan du følge summationsformlen, hvilket øger effekten for hvert udtryk., Men det er ret nemt at bare følge mønstrene.
k-værdierne i “n vælg k” begynder med k=0 og stiger med 1 i hvert udtryk. Det sidste udtryk skal ende med n lig med k, i dette tilfælde n=3 og k=3.
Dernæst skal vi tilføje kræfterne på (2 and) og (-3).
tændingen (2.) begynder med n-værdien, så i dette tilfælde 3, og vil falde med 1 på hvert udtryk, indtil du kommer til nul. Tændingen (-3) starter med nul og øges med en hver gang, indtil du kommer til n eller 3 i dette problem.,

Fordi nogen værdi opløftet til nul power er lig med 1, kan du forenkle vilkårene med beføjelser til nul.

Næste gå videre og anvende de beføjelser, og at forenkle, hvor det er muligt.,

Den Pascal ‘ s Trekant Genvej

Den sidste del er at løse de kombinationer formel. Den indlysende måde at gøre dette på er at anvende kombinationsformlen for hvert problem. Men vi tager en fin lille genvej her ved hjælp af Pascals trekant.
Pascals trekant er en simpel, men kraftfuld trekant dannet ved at oprette en trekant med tre 1 ‘ er til at begynde., For hver række derefter du blot skrive 1 er i begge ender, og finde den midterste tal(r) ved at tilføje de to værdier fra direkte over det.

Nu her er den gode del. Skjult i Pascals trekant er alle svarene på enhver”n vælg k”! Det er som et hemmeligt lille snydeark!
diagrammet nedenfor viser dig, hvor de skjulte “n vælg k ‘er” er placeret.,

For vores problem, vi skal løse for: 3 at vælge 0, 3 1, 3 vælg 2 og 3 for at vælge 3. Hvilket er alle værdierne i 4. række. Så alt, hvad vi skal gøre, er at se på 4.række af Pascals trekant og matche svarene.
den 4.række har værdierne: 1, 3, 3, 1. Så jeg vil bare erstatte i svarene til vores n vælg K ‘ er.,

endelig er alt hvad du skal gøre multiplicere og forenkle hvert udtryk ned til dets enkleste form. Glem ikke at tjekke dit endelige svar for at sikre, at kræfterne på hvert udtryk stadig tilføjer graden af din originale binomial! Tro mig, det er utroligt nemt at lave en transskription fejl i denne type af problem 😉
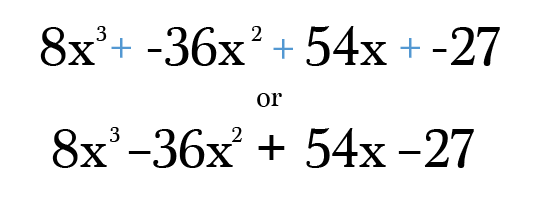
har Brug for et andet eksempel?,
i videoen ovenfor viser jeg dig, hvordan du bruger Binomial – sætningen til at udvide binomial (⁵- 3y)vejret. Plus jeg viser dig nogle ekstra tricks til at blive organiseret og et par hurtige kontroller, du kan bruge til nemt at identificere almindelige fejl.
tak for læsning!
STAY Hold forbindelsen <
Hold dig opdateret med alt Math Hacks er op til!