Logaritmiske funktioner er den inverse af eksponentielle funktioner. Det omvendte af den eksponentielle funktion y = A.er ay = ay. Den logaritmiske funktion y = Loga.er defineret til at svare til den eksponentielle ligning = = ay. y = Loga.kun under følgende betingelser: = =ay, a > 0 og A 1 1. Det kaldes den logaritmiske funktion med base a.
overvej hvad det inverse af den eksponentielle funktion betyder: = = ay., Givet et tal and og en base a, til hvilken magt y Skal a hæves til lige x? Denne ukendte eksponent, y, er lig med Loga.. Så du ser en logaritme er intet mere end en eksponent. Per definition, aloga.==, for hver reel <> 0.
Nedenfor er afbilledet grafer af formen y = logax når en > 1, og når 0 < < 1. Bemærk, at domænet kun består af de positive reelle tal, og at funktionen altid øges, når.øges.,
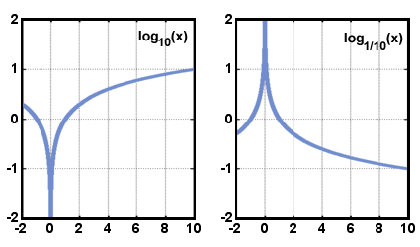
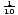 x.
x.domænet af en logaritmisk funktion er reelle tal, der er større end nul, og området er reelle tal. Grafen for y = Loga. er symmetrisk med grafen for y = A.med hensyn til linjen y=.. dette forhold gælder for enhver funktion og dens inverse.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(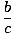 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
En naturlig logaritmisk funktion er en logaritmisk funktion med base e. f (x) = logex = ln x, hvor x > 0. ln. er bare en ny form for notation for logaritmer med base e.de fleste regnemaskiner har knapper mærket “log” og “ln”. Knappen “log” antager, at basen er ti, og knappen” ln ” lader selvfølgelig basen være lig med e., Den logaritmiske funktion med base 10 kaldes undertiden den fælles logaritmiske funktion. Det bruges bredt, fordi vores nummereringssystem har base ti. Naturlige logaritmer ses oftere i calculus.
Der findes to formler, der gør det muligt at ændre basen af en logaritmisk funktion. Den første siger dette: logab = 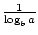 . Den mere berømte og nyttige formel til ændring af baser kaldes almindeligvis ændringen af basisformlen. Det gør det muligt at ændre basen af en logaritmisk funktion til ethvert positivt reelt tal 1 1. Det hedder, at Loga. =
. Den mere berømte og nyttige formel til ændring af baser kaldes almindeligvis ændringen af basisformlen. Det gør det muligt at ændre basen af en logaritmisk funktion til ethvert positivt reelt tal 1 1. Det hedder, at Loga. = 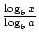 ., I dette tilfælde er a, B og 1 alle positive reelle tal og A, B 1 1.
., I dette tilfælde er a, B og 1 alle positive reelle tal og A, B 1 1.
i det næste afsnit diskuterer vi nogle anvendelser af eksponentielle og logaritmiske funktioner.