“enhedscirklen” er en cirkel med en radius på 1.
at være så enkel, det er en fantastisk måde at lære og tale om længder og vinkler.
midten er sat på en graf, hvor axis-aksen og Y-aksen krydser, så vi får dette pæne arrangement her.
Sinus, Cosinus og Tangens
Fordi radius er 1, kan vi direkte måle sinus, cosinus og tangens.,
Hvad sker der, når vinklen, θ, 0°?
cos 0° = 1, synd 0° = 0 og tan 0° = 0
Hvad sker der, når θ er 90°?
cos 90° = 0, synd 90° = 1 og tan 90° er udefineret
Prøv Det Selv!
prøv!, Flyt musen rundt for at se, hvordan forskellige vinkler (i radianer eller grader) påvirker sinus, cosinus og tangent
“siderne” kan være positive eller negative i henhold til reglerne for kartesiske koordinater. Dette gør sinus, cosinus og tangent skift mellem positive og negative værdier også.
prøv også den interaktive enhedscirkel.,
Pythagoras
Pythagoras’ Læresætning siger, at for en retvinklet trekant, kvadrat af den lange side er lig summen af kvadraterne på de to andre sider:
x2 + y2 = 12
Men 12 er kun 1, således:
x2 + y2 = 1
(ligningen for cirklen)
Også, da x=cos y=sin, får vi:
(cos(θ))2 + (sin(θ))2 = 1
en nyttig “identitet”
Vigtige Vinkler: 30°, 45° og 60°
Du bør forsøge at huske, sin, cos og tan for de vinkler, 30°, 45° og 60°.,
Ja, ja, det er en smerte at skulle huske ting, men det vil gøre livet lettere, når du kender dem, ikke kun i eksamener, men andre gange, når du skal lave hurtige estimater osv.
Dette er de værdier, du skal huske!,id=”0f47f3223b”>
What about tan?,
Nå, tan = sin/cos, så kan vi beregne det som dette:
tan(30°) =sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sin(60°)cos(60°) = √3/21/2 = √3
* Bemærk: skrivning af 1√3 kan koste dig varemærker (se Rationel Nævnere), så i stedet bruge √33
en Hurtig Skitse
en Anden måde at hjælpe dig med at huske 30° og 60° er at lave en hurtig skitse:
| Tegn en trekant med sidelængderne 2 | 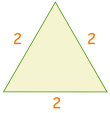 |
|
|
Skåret i halve.,div id=”56c966b492″> Eksempel: sin(30°)Sinus: sohcahtoa sinus er modsatte, divideret med hypotenusen
sin(30°) = oppositehypotenuse = 12
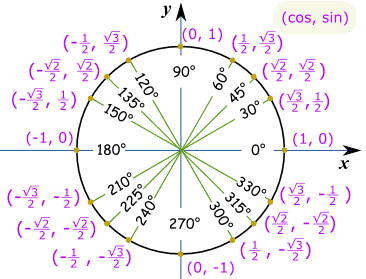
Den Hele CirkelFor hele kredsen, vi har brug for værdier i hver kvadrant, med den korrekte plus-eller minustegn, som pr Retvinklede Koordinater: Bemærk, at cos er først og synd er, for det andet, så det går (cos, synd):
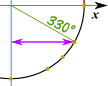
Gem som PDF Eksempel: Hvad er cos(330°) ?,
lav en skitse som denne, og vi kan se, at det er den “lange” værdi: √32 Og det er det samme enhedscirklen i radianer.
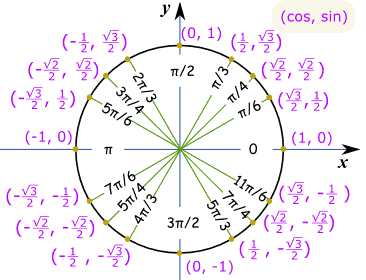
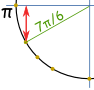
eksempel: Hvad er synd (7/ / 6) ?
tænk “7./6 = + + 6 / 6”, lav derefter en skitse. Vi kan derefter se, at det er negativt og er den “korte” værdi − –< |