Indhold – Konstant acceleration

Indhold

Konstant acceleration

Vi er alle bekendt med det faktum, at en bil hastigheder op, når vi sætter vores fod på speederen. Hastigheden af ændring af hastigheden af en partikel med hensyn til tid kaldes dens acceleration. Hvis partikelhastigheden ændres med en konstant hastighed, kaldes denne hastighed den konstante acceleration.,for eksempel, hvis hastigheden af en partikel, der bevæger sig i en lige linje, ændres ensartet (med en konstant ændringshastighed) fra 2 m/s til 5 m/s over et sekund, er dens konstante acceleration 3 m/s\(^2\).

Faldende hastighed

Hvis en partikel har en indledende hastighed på 6 m/s og en konstant acceleration af \(-2\ m/s\(^2\), så er:

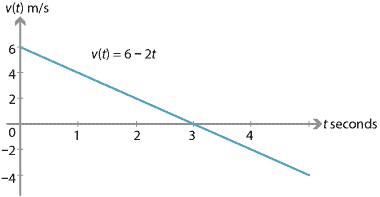
i Løbet af de første tre sekunder, partikel ‘ s hastighed er aftagende (partikel er aftagende). Efter tre sekunder er partiklen øjeblikkeligt i ro., Efter tre sekunder falder hastigheden stadig, men hastigheden øges (partiklen går hurtigere og hurtigere).

Oversigt

Hvis vi antager, at den procentvise ændring af anslagsstyrken (acceleration) er en konstant, så er den konstante acceleration er givet ved

\

Mere præcist, den konstante acceleration \(a\) er givet ved formlen

\

, hvor \(v(t_i)\) er hastigheden i tid \(t_i\). Da hastighed er en vektor, så er acceleration.,

de konstante accelerationsformler til bevægelse i en lige linje

i hele dette afsnit har vi overvejet bevægelse i en lige linje med konstant acceleration. Denne situation er meget almindelig; for eksempel bevæger en krop, der bevæger sig under tyngdekraftens indflydelse, med en konstant acceleration.

det antages, at bevægelsen begynder, når \(t = 0\), og at den oprindelige position tages som Oprindelse, det vil sige \(\(0) = 0\).,

De fem bevægelsesligninger

1. \(v = u + i\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}på^2\)
4. \(v^2 = u^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}på^2\)

Bemærk. Hver af de fem ligninger involverer fire af de fem variabler \(u, v,., A, t\). Hvis værdierne for tre af variablerne er kendt, kan de resterende værdier findes ved at bruge to af ligningerne.,

afledt af konstantaccelerationsformlerne

den første bevægelsesligning

da accelerationen er konstant, har vi \(a = \dfrac{v-u}{t}\). Dette giver den første bevægelsesligning, \(v = u + at\).

den anden bevægelsesligning

den anden ligning,

\

siger, at forskydning opnås ved at multiplicere gennemsnittet af de indledende og endelige hastigheder med den tid, der er gået under bevægelsen. Mere enkelt:

\

Vi kan udlede denne ligning ved hjælp af det faktum, at forskydningen er lig med det underskrevne område under hastigheds–tidsgrafen.,

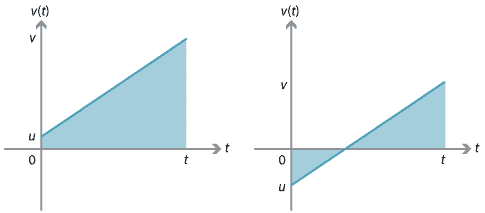
for grafen til højre kan forskydningen findes ved at overveje de to trekanter mellem grafen og \(t\)-aksen. En af trekanterne har positivt underskrevet område, og den anden har negativt underskrevet område.

at finde forskydningen af en partikel fra hastigheds–tidsgrafen ved hjælp af integration vil blive diskuteret i et senere afsnit af dette modul.,

Den tredje ligning af bevægelse

stedet for \(v\) fra første ligning til anden ligning giver

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+i)t}{2} \\ &= \dfrac{2ut+i^2}{2} \\ &= ut + \dfrac{1}{2}på^2, \end{align*}

, som er den tredje ligning. Derfor er \(\ \ ) en kvadratisk i \(t\), og derfor er grafen af \(\ \) mod\ (t\) en parabola.

den fjerde bevægelsesligning

fra den første ligning har vi \(t = \dfrac{v-u}{a}\)., At erstatte denne ind i den anden ligning giver

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{juster*}

omarrangering for at gøre \(v^2\) motivet producerer den fjerde ligning: \(v^2 = u^2 + 2A.\).

den femte bevægelsesligning

fra den første ligning har vi \(u = v-at\)., Ved hjælp af den anden ligning, får vi

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-i+v)t}{2} \\ &= \dfrac{2vt-i^2}{2} \\ &= vt-\dfrac{1}{2}på^2, \end{align*}

, som er den femte i en ligning.

lodret bevægelse

bevægelse på grund af tyngdekraften er en god kontekst til at demonstrere brugen af konstantaccelerationsformlerne., Som tidligere omtalt er vores to retninger i lodret bevægelse op og ned, og der skal træffes beslutning om, hvilken af de to retninger der er positiv. Acceleration på grund af tyngdekraften er en konstant, med størrelse betegnet med \(G\). I det følgende eksempel tager vi opadgående retning for at være positiv og tager \(g = 10\) m/s\(^2\).

Yderligere brug af bevægelsesligninger

Next page – Content – Average velocity and average speed