Find Alle Rødder af et Polynomium Funktion
Brug vpasolve for at finde alle løsninger til den funktion f(x)=6×7-2×6+3×3-8.
syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)
vpasolve returnerer syv rødder i den funktion, som forventet, fordi funktionen er et polynomium af grad syv.,
Find nuller af en ikke-polynomisk funktion ved hjælp af søgeområder og udgangspunkter
et plot af funktionen f (.)=e (. / 7)cos(2.) afslører periodiske nuller med stigende skråninger ved nulpunkterne, når as øges.
syms xh = fplot(exp(x/7)*cos(2*x),);grid on
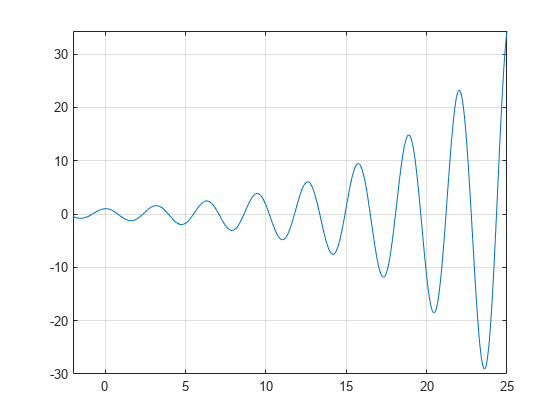
Brug vpasolve for at finde et nulpunkt for funktionen f. Bemærk, at vpasolve returnerer kun en opløsning af en ikke-polynomisk ligning, selvom der findes flere løsninger., On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true)end
ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')
ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')
ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')
To find a zero close to x=10, set the starting point to 10.,
vpasolve(f,x,10)
ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')
for At finde nul tæt på x=1000, sæt udgangspunkt for at 1000.
vpasolve(f,x,1000)
ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')
for At finde nul i intervallet 15≤x≤25, sæt søg udvalg til .,
vpasolve(f,x,)
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
for At finde flere nuller i intervallet du kan ikke ringe vpasolve gentagne gange, fordi det giver samme resultat på hvert opkald, som tidligere vist. I stedet skal du indstille søgeområdet og indstille 'Random' til true.,
for k = 1:3 vpasolve(f,x,,'Random',true)end
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')
Fordi 'Random' vælger udgangspunkter tilfældigt, at den samme løsning kan findes på hinanden følgende opkald.,
Finde Alle Nuller i det Angivne søgeområde
Opret en funktion findzeros til systematisk at finde alle nuller for f i en given søgning interval, inden for en bestemt fejl tolerance. Funktionen starter med inputsøgningsområdet og kalder vpasolve for at finde et nul. Derefter opdeler det søgeområdet i to omkring nulværdien og kalder rekursivt sig selv med de nye søgeområder som input for at finde flere nuller.
funktionen forklares afsnit for afsnit her.,
Angiv funktionen med de tre indgange og en udgang. Den første indgang er funktionen, den anden indgang er området, og den valgfri tredje indgang giver dig mulighed for at angive fejlen mellem et nul og de højere og nedre grænser, der genereres fra den.
function sol = findzeros(f,range,err)
Hvis du ikke angive den valgfrie argument for fejl tolerance, findzeros sæt err til 0.001.
if nargin < 2 err = 1e-3;end
Find et nul i søgeområdet ved hjælp af vpasolve.,
sol = vpasolve(f,range);
Hvis vpasolve ikke finder et nul, Afslut.
if(isempty(sol)) return
Hvis vpasolve finder et nul, split søg udvalg i to søgning spænder over og under nul.
else lowLimit = sol-err; highLimit = sol+err;
Call findzeros med det lavere søgeområde. Hvis findzeros returnerer nuller, skal du kopiere værdierne til løsningsarrayet og sortere dem.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end
Call findzeros med det højere søgeområde., Hvis findzeros returnerer nuller, skal du kopiere værdierne til løsningsarrayet og sortere dem.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend
hele funktionen findzeros er som følger. Gem denne funktion som findzeros.m i den aktuelle mappe.
syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'
Få Løsninger til udførelse af Vilkårlig Præcision
Brug digits for at angive præcision af de løsninger, der returneres af vpasolve., Som standard returnerervpasolve løsninger til en præcision på 32 signifikante tal.
f = exp(x/7)*cos(2*x);vpasolve(f)
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
Brug digits for at øge præcisionen til 64 betydende cifre. Når du ændrer digits, skal du sikre dig, at du gemmer den aktuelle værdi, så du kan gendanne den.,
digitsOld = digits;digits(64)vpasolve(f)
ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')
Næste, kan du ændre præcision af løsninger til 16 betydende cifre.
digits(16)
Løs Multivariate ligninger ved hjælp af søgeområder
overvej følgende ligningssystem.
==10(cos (+)+cos(y)))=.+y2-0.1 .2y. + y-2.7 = 0
et plot af ligningerne for 0 0. 2.5 2.5 og 0.. 2.5 2.5 viser, at de tre overflader skærer hinanden i to punkter., For bedre at visualisere plottet skal du bruge view. For at skalere colormap-værdierne skal du bruge caxis.
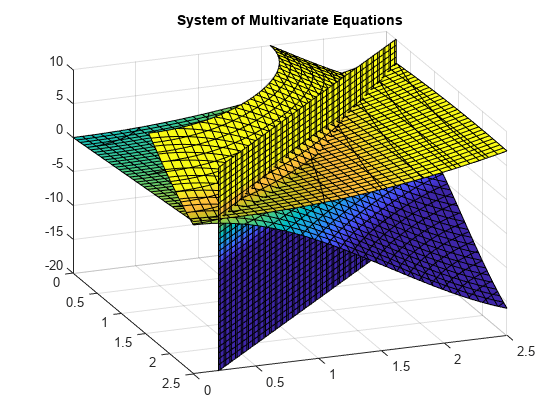
Brug vpasolve for at finde et punkt, hvor de overflader, skærer hinanden. Funktionen vpasolve returnerer en struktur. For at få adgang x-, y – og z-værdier af den løsning, indeks i strukturen.,
sol = vpasolve(equations);
for at søge i et område af løsningsrummet skal du angive søgeområder for variablerne. Hvis du angiver intervallerne 0 0 1.5 1.5 1,5 og 1,5 y y 2.5 2,5, søger vpasolve funktionen i det afgrænsede område, der vises.

Brug vpasolve for at finde en løsning for denne søgning rækkevidde. For at udelade et søgeområde for z skal du indstille det tredje søgeområde til .,
vars = ;range = ;sol = vpasolve(equations, vars, range);
for At finde flere løsninger, sætte 'Random' mulighed for at true. Dette gør vpasolve brug tilfældige udgangspunkter på successive kørsler. Indstillingen 'Random' kan bruges sammen med søgeområder til at lave vpasolve brug tilfældige udgangspunkter inden for et søgeområde. Fordi 'Random' vælger udgangspunkter tilfældigt, kan den samme løsning findes på successive opkald., Ring til vpasolve gentagne gange for at sikre, at du finder begge løsninger.
Plot ligningerne. Overlejre løsningerne som et scatter plot af punkter med gul X markører ved hjælp af scatter3. For bedre at visualisere plottet skal du gøre to af overfladerne gennemsigtige ved hjælp af alpha. Skal farvekortet til plotværdierne ved hjælp af caxis, og skift perspektivet ved hjælp af view.
vpasolve finder løsninger ved skæringspunktet mellem overfladerne dannet af ligningerne som vist.,

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)