På disse sider ser vi på nogle interessante koncepter, ser vi på, krumme rum: hvad krumme rum betyder, hvordan vi kan fortælle, hvis en plads er buet indefra eller udefra.
Vi ser på, hvordan vi kan integrere på type plads inde i en anden og se, at vi kan kortlægge mellem forskellige rum på forskellige måder.
Vi ser også på komprimering, og hvordan vi kan repræsentere uendeligt store og uendeligt små vektorer i vores rum på måder, der ikke fører ikke til singulariteter og andre problemer.,
disse begreber viser sig at være nyttige, selv når vi arbejder med fladt rum, finder vi måder at repræsentere vektorer og fly, der ikke går gennem oprindelsen. Dette giver os måder at repræsentere rotationer og oversættelser som en enkelt operation.
den anden applikation er relativistisk rumtid.
Rienmannian Geometry
i Rienmannian geometry rummet kan kurve på forskellige steder (se manifolds) her ser vi på geometrier, hvor kurven for rummet er konstant.,
Eulidean Geometri
fladskærms plads
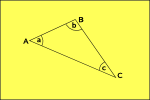
Hyperbolsk Geometri
plads kurver udad
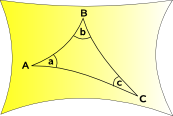
Sfærisk Geometri og Elliptisk Geometri
plads kurver indad
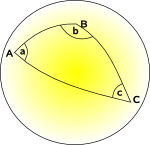
I en buet (Ikke-Euklidisk) geometri, vi kan ikke finde et sæt koordinater, der er indbyrdes vinkelrette, hvor koordinere linjer, der alle er parallelle med hinanden, og hvor hver grid-pladsen har samme område., Vi kan muligvis finde et koordinatsystem, hvor vi kan gøre nogle af disse, men ikke alle.
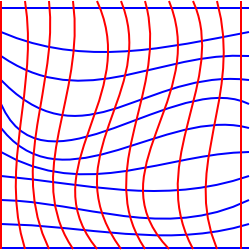
dette diagram forsøger at illustrere denne situation i 2 dimensioner, selvom det er lidt vildledende, fordi vi har tegnet det på et plan, så vi kunne have tegnet rektangulære koordinater.
for at forsøge at illustrere en situation, hvor det er umuligt, vi kunne tænke på en todimensionel plan, som er blevet strakt ind i den tredje dimension.,

I denne situation kan vi vælge koordinater, der udgør et rektangulært gitter, når der projiceres op på en vandret plan, men til en person, der bor i overfladen, så nogle af de tern, vil synes at have et større område end andre, og gitterlinjer kan vises ikke at være parallelle. Der er ikke noget todimensionelt koordinatsystem, der bevarer parallelle linjer, vinkler og områder på samme tid.,
et lignende eksempel forsøger at kortlægge jordens overflade, vi kan bruge breddegrader og længdegrader, men længdegraderne kommer tættere på polerne.
i disse tilfælde kunne vi arbejde med hensyn til 3-dimensionelle koordinater, og det er en tilgang, vi vil tage med nogle typer ikke-euklidiske geometrier. Det er ofte muligt at indlejre en bestemt geometri i en højere dimensionel geometri for at gøre det mere euklidisk.,
det er undertiden tilfældet, at når vi ser på en geometri i stor skala, at det er ikke-euklidisk, men hvis vi ser på det i mindre og mindre skala, så nærmer det sig en euklidisk geometri. For at gøre dette er vi nødt til at finde et koordinatsystem, hvor vinkler bevares på hvert punkt, det vil sige, at de vandrette og lodrette koordinatlinjer altid skal krydse hinanden ved 90., selvom linjerne muligvis ikke er lige. Dette er kendt som en konform geometri. I denne type geometri kan vi i det mindste definere et lokalt koordinatsystem.,
relateret til dette er, om geometrien kan differentieres og integreres, en betingelse for dette er, at den skal være velopdragen og ikke have pludselige spring osv. Nogle geometrier og koordinatsystemer kan være velopdragen nogle steder, men har singulariteter osv.
for diskussion om, hvordan krumning måles se denne side.
matematisk Notation
hvordan håndterer vi geometrier, hvor vi ikke kan bruge alle de regler, der gælder for euklidisk geometri?,
en tilgang er at bruge tensor notation, dette giver konventioner og notation, som hjælper os med at skifte mellem forskellige koordinatsystemer. Et ortogonalt koordinatsystem, lokalt til ethvert punkt, kan defineres ved hjælp af basisvektorer, der er tangenter til koordinatlinjerne.,Manifold
se denne side
Forholdet mellem Hyperbolsk og Minkowski Geometrier
| Minkowski Geometri | Hyperbolsk Geometri | |
| punkt | begivenhed i rum tid | partikel i ensartet bevægelse |
| afstanden mellem to punkter | plads-tidsintervallet mellem to begivenheder | relative hastighed mellem to sådanne partikler |
Terminologi
Her ser vi på den terminologi, som geometrier, rum, modeller, prognoser og forvandler., Dens ganske vanskeligt, når vi begynder at beskæftige sig med ikke-euklidisk geometrier, fordi vi bruger lignende terminologi, som vi er vant til i konventionelle euklidisk rum, men vilkårene kan have lidt forskellige egenskaber.,prøv
Elliptisk Geometri
Modeller
her er nogle Eksempler:
- Øvre halvdel-fly model
- Poincare disc-modellen
- Projektiv model
- Konform model
Fremskrivninger
Stereografisk Projektion
Forvandler
Invariant
her er nogle Eksempler:
- Möbius Omdanne
- Lorentz Omdanne
Parallel-Postulat
Hvis vi tager væk parallel-postulat fra Euklidisk Rum.,
dette fører til:
- parallelt postulat er falsk
- vinklerne i en trekant tilføjer ikke til
- for en form af en given størrelse eksisterer der generelt ikke en lignende form af en større størrelse.,ctive
konform (Poincaré disc ) lige linjer – geodesics segmenter af cirkler angle bevare mere indre vinkler i trekant π-(α+β+γ)=CΔ afstanden mellem to punkter med