
Har du nogensinde spekulerer på, hvordan kan det sne på over frysepunktet temperaturer? Nå, den naive forklaring er, at det simpelthen tager tid for snefnugene at smelte, når de trænger ind over fryseluften, når de falder nedad til jorden. Dette er selvfølgelig grunden til, at hagl kan falde i varmt vejr. Haglsten falder simpelthen hurtigt, for hurtigt til at lade den varme luft smelte Haglen. Dette er dog ikke den vigtigste forklaring på, hvorfor det kan sne, når det er over frysepunktet.,
fra nedenstående figur er det tydeligt, at der er en klar afhængighed af fugtigheden – jo tørrere det er, jo varmere kan det være under sner. Dette indebærer, at hovedfaktoren, i det mindste under tørre forhold, har at gøre med fugtighed. Og denne faktor er fordampning. Mere specifikt, når snefnugene falder ned, fordamper de. Denne proces tager varme og holder flagerne kolde.
så hvis vi ønsker at beregne den maksimale temperatur, er vi nødt til at estimere til netto varmebalance af flage. For det første, når flagerne rejser i et varmt miljø, får de varme fra omgivelserne gennem ledning., For det andet bruges varme til at fordampe flagerne og derved afkøle dem. Hvis fordampningsvarmen “sink” er større end varmeledningen, forbliver flagerne frosne.
det viser sig, at dette let kan beregnes. Nej, det er ikke nemt at beregne varmeledningen eller fordampningsvarmen, men forholdet er, da forskellige ukendte geometriske faktorer annullerer.
Hvis du er ligeglad med beregningen (fordi du ikke er en videnskabsfreak), kan du blot besøge lommeregnersiden.
Hvis du er ligeglad, her er afledningen., Antag, at strømmen omkring flagerne er sådan, at der dannes et grænselag af bredde d omkring det. Den samlede varmestrøm $F_H$ til at flage (fx, J/sek i MKS) vil være givet ved Fourier ‘ s lov:
hvor $\kappa$ er den varme diffusion coefficient of air (fx, m2/sek i MKS), c er varmekapacitet for luft (J/kg i MKS), A er arealet af grænselag omkring flake, mens ΔT er temperaturforskellen mellem flake og miljø.,
Ligeledes kan man bruge Fick ‘ s lov for at opnå diffusion af vanddamp fra flake (hvor temperaturen er tæt på frysepunktet, og den relative fugtighed er 100%), at det omgivende miljø, hvor temperaturen er højere, og den relative luftfugtighed er lavere:
her er D vanddiffusionskoefficienten (f.eks. m2/SEK i MKS) og m2 er vanddampdensiteten (kg/m3 i MKS).,
den fordampende is kræver varme, så hvis der er en vanddampmasseflu.af Φ fra flaken, ville det kræve varme med en hastighed på $F_. = \epsilon \Phi$ hvor $\epsilon$ er varmen af fordampning af is (J/kg i MKS).
højeste temperatur, over hvilken snefnug smelter, er den temperatur, som de to varmestrømme er den samme:
Bemærk, at geometrien af strømmen omkring flaken annullerer, fordi begge varmeflu .er afhænger af d og A på samme måde., Dette ville også være tilfældet, hvis grænselaget omkring flaken er komplekst, så d faktisk afhænger af retningen. Derfor
hvor $\rho_{sat}$ er mætning vanddamp tæthed.
tilslutning af tallene (som kan findes for eksempel i CRC handbook of chemistry and physics), resultater med en implicit ligning for temperaturenfordi mætning vanddamp densitet afhænger af temperaturen så godt., Vi kan forenkle tingene, hvis vi i stedet spørger, hvad der er den relative fugtighed, der kræves for at holde flaken frosset ved en given temperatur. Det er:
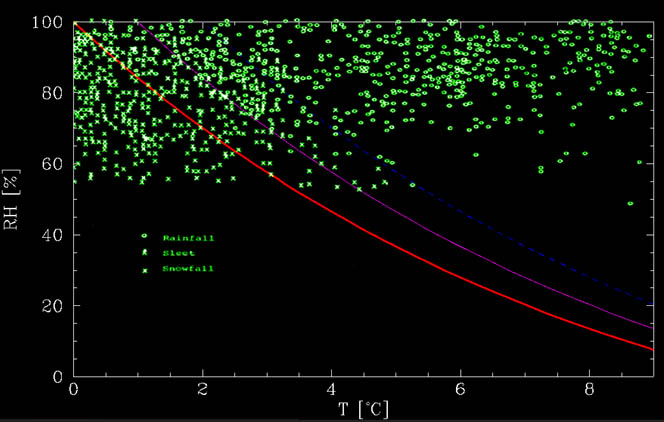
hvor $T_C$ er temperaturen i grad celsius. denne funktion kan ses i nedenstående figur sammen med data fra Matsuo og Sasyo, 1981. Som det fremgår af figuren, er den beregnede graf omtrent den nedre grænse, under hvilken der ikke er nogen regn overhovedet. Ved varmere temperaturer er der en blanding., Op til ca. 1 above C over Ingen smeltelinie, er der for det meste sne mens mellem ca.1 and C og 2. C over linjen, er det for det meste regn, men sne er muligt. Disse begivenheder kan skyldes yderligere effekter, såsom stærke do .ndrafts, tid det tager at smelte sneen osv.
hvis vi ønsker at observere varmt vejr sne, er meget tørre forhold påkrævet. For eksempel, hvis jordfugtigheden kun er omkring 20% (meget sjælden, fordi hvis der er nedbør, er atmosfæren generelt våd!) så kunne det sne ved 8.C (eller 46. f for engelske brugere).,
Et andet krav er, at ingen steder langs nedstigningen overgår luften ingen smeltelinie. Hvis det gør det, smelter flaken selvfølgelig.
Hvis temperaturen stiger over frysepunktet, er der der er ingen parametre, som typen af nedbør kan bestemmes for sikkerhed. Alt, hvad vi derefter kan forudsige, er sandsynligheden for, at sne faktisk falder. Dette kan gøres ved hjælp af resultaterne fra H .ggmark og Ivarsson (1997), kun korrigeret for at bruge frosne pærer og ikke vådpæretemperaturen.
bundlinjen er en lommeregner, som sandsynligheden for sne kan estimeres med.,