tværsnit

Ejendomme i Områder

Barycentrum

barycentrum af en form repræsenterer det punkt, om hvilket område af afsnittet er jævnt fordelt. Hvis området er dobbelt symmetrisk omkring to ortogonale akser, ligger centroiden i skæringspunktet mellem disse akser. Hvis området er symmetrisk omkring kun en akse, ligger centroiden et sted langs den akse (den anden koordinat skal beregnes)., Hvis den nøjagtige placering af barycentrum ikke kan bestemmes ved inspektion, kan det beregnes ved:

hvor dA repræsenterer området med en forsvindende lille del, A er det samlede areal af tværsnittet, og x og y koordinaterne for element dA med hensyn til den akse, der er af interesse.,

de centroidale placeringer af fælles tværsnit er veldokumenterede, så det er typisk ikke nødvendigt at beregne placeringen med ligningerne ovenfor., af grundformer, hvis centroidal steder er kendt med hensyn til nogle reference punkt, så centroidal placering af sammensat på tværs af afsnit, kan beregnes som:

hvor xc,jeg og yc,jeg er den rektangulære koordinater centroidal placering af det i ‘te punkt med hensyn til referencepunktet, og Ai er den i’ te afsnit.,

Centroidal afstand

den centroidale afstand, c, er afstanden fra centroidet i et tværsnit til den ekstreme fiber., Den centroidal afstanden i y-retning for et rektangulært tværsnit er vist i figuren nedenfor:

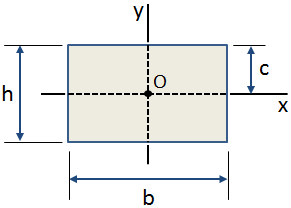
Fælles formål for centroidal afstand er:

• beregningen af den maksimale bøjning stress i et tværsnit
• beregningen af værdien af det første øjeblik af området, Q, over et punkt i tværsnittet for at afgøre, shear stress på det punkt

Første Øjeblik af Området

Det første øjeblik af et område med hensyn til en akse af renter beregnes som:

Qx = ∫ y dA

Qy = ∫ x dA

hvor Qx er det første øjeblik, om x-aksen og Qy er det første øjeblik, om y-aksen.,Hvis området er sammensat af en samling af grundlæggende former, hvis centroidal steder er kendt med hensyn til den akse, der er af interesse, så er det første øjeblik af den sammensatte område kan beregnes som:

Bemærk, at det første øjeblik af det område, der er brugt ved beregning af barycentrum af et tværsnit med hensyn til visse produkter (som tidligere omtalt)., Det første øjeblik bruges også til beregning af værdien af forskydningsspænding på et bestemt punkt i tværsnittet. I dette tilfælde beregnes det første øjeblik for et område, der udgør en mindre del af tværsnittet, hvor området er afgrænset af interessepunktet og den ekstreme fiber (top eller bund) af tværsnittet. Det første øjeblik beregnes om en akse, der passerer gennem tværsnittets centroid.,

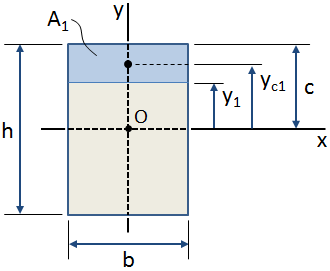
i figuren ovenfor er det skraverede blå område det interesseområde inden for det samlede tværsnit.,nt af dette område med hensyn til x-aksen (der passerer gennem tværsnittet barycentrum, punkt O i ovenstående figur) beregnes som:

Hvis centroidal placering af det område af interesse er kendt, så er det første øjeblik af området med hensyn til den akse, kan beregnes som (se ovenstående figur):

Det skal bemærkes, at det første øjeblik af et område vil være positiv eller negativ afhængig af placeringen af den holdning af området med hensyn til den akse, der er af interesse., Derfor vil det første øjeblik af hele området af et tværsnit med hensyn til sin egen centroid være nul.

Område Inertimoment

Det andet øjeblik af området, mere almindeligt kendt som inertimoment, jeg, af et tværsnit er en indikation af strukturel medlems evne til at modstå bøjning.,(Note 1) Ix og Iy er de øjeblikke af inertimoment om x – og y – akser, henholdsvis, og er beregnet ved:

Ix = ∫ y 2 dA

Iy = ∫ x2 dA

hvor x og y koordinaterne for element dA med hensyn til den akse, der er af interesse.

oftest beregnes inertimomenterne med hensyn til sektionens centroid. I dette tilfælde betegnes de som centroidale inertimomenter og betegnes som IC.for inertien omkring x-aksen og iskald for inertien omkring y-aksen.,

inertimomenterne i fælles tværsnit er veldokumenterede, så det er typisk ikke nødvendigt at beregne dem med ligningerne ovenfor. Egenskaber for flere fælles tværsnit er angivet i slutningen af denne side.

Hvis et tværsnit er sammensat af en samling af grundlæggende former, hvis centroider alle er sammenfaldende, er inertimomentet i det sammensatte afsnit simpelthen summen af de individuelle inertimomenter. Et eksempel på dette er en kassebjælke, der består af to rektangulære sektioner, som vist nedenfor., I dette tilfælde har det ydre afsnit “positivt område”, og det indre afsnit har” negativt område”, så det sammensatte inertimoment er subtraktionen af inertimomentet i det indre afsnit fra det ydre afsnit.

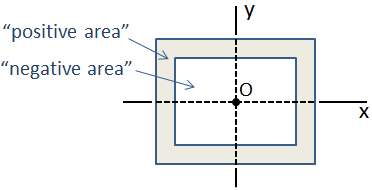
I tilfælde af en mere kompliceret sammensat på tværs af afsnit, hvor centroidal steder er ikke sammenfaldende, inertimoment og kan beregnes ved hjælp af parallel-akse sætning.

det er vigtigt ikke at forveksle inertimomentet i et område med massemomentet af inerti i et fast legeme., Området inertimoment indikerer et tværsnit modstand mod bøjning, mens masse inertimoment indikerer et legeme modstand mod rotation.,

Parallel-Akse Sætning

Hvis inertimoment af et tværsnit om en centroidal akse er kendt, så den er parallel akse sætning kan bruges til at beregne inertimoment om nogen parallel-akse:

hvor Ic er inertimoment om centroidal akse, d er afstanden mellem centroidal-aksen og parallel-akse, og A er arealet af et tværsnit.,

Hvis et tværsnit er sammensat af en samling af grundformer, hvis centroidale inertimomenter er kendt sammen med centroidernes afstande til et eller andet referencepunkt, kan den parallelle akse-sætning bruges til at beregne inertimoment for det sammensatte tværsnit.

for eksempel kan en I-stråle tilnærmes med 3 rektangler, som vist nedenfor. Da dette sammensatte afsnit er symmetrisk omkring både section – og y-akserne, kan sektionens centroid placeres ved inspektion i skæringspunktet mellem disse akser. Centroid er placeret ved oprindelsen, O, i figuren.,

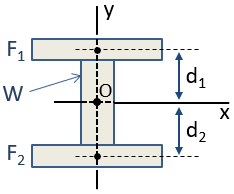
træghedsmomentet for det sammensatte afsnit kan beregnes ved hjælp af den parallelle akse-sætning. Sektionens centroidale inertimoment omkring IC-aksen, IC., beregnes som:

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

Egenskaber Fælles på Tværs af Sektioner

tabellen nedenfor giver egenskaber fælles på tværs af sektioner. Mere omfattende tabeller findes i de angivne referencer.

egenskaberne beregnet i tabellen inkluderer areal, centroidal inertimoment, sektionsmodul og gyrationsradius.,

Noter

Bemærk 1: Nedbøjning af Bjælken

nedbøjning af bjælken under bøjning bestemmes af inertimoment af tværsnit, længden af bjælken, og den elastiske modulus af materialet. Flere detaljer er givet i denne diskussion af stråle afbøjning.