beginnen wir mit einem einfachen Beispiel, sagen wir, wir möchten zu multiplizieren out (2x-3)3. Dies wäre nicht zu schwierig, lange Hand zu tun, aber lassen Sie uns den Binomialsatz verwenden, so dass, wenn Sie größere Erweiterungen wie Binome auf die 4, 5, 6, … Kräfte erhöht begegnen Sie genau wissen, was zu tun ist.
Um loszulegen, müssen Sie die beiden Begriffe aus Ihrem Binom (die x-und y-Position unserer obigen Formel) und die Potenz (n) identifizieren, auf die Sie das Binom erweitern.,
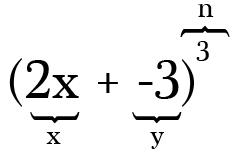
Beispiel: zu erweitern (2x-3)3, die beiden Begriffe sind 2x und -3 und die power -, oder n-Wert ist 3. Beachten Sie, dass es nicht so wichtig ist, immer dann, wenn Sie eine Subtraktion in Ihrem Binom haben, daran zu denken, das Minus als negatives Symbol in den begleitenden Begriff aufzunehmen.
Das Wunderbare am Binomialsatz ist, dass wir das erweiterte Polynom finden können, ohne eine Reihe von Binomen zu multiplizieren. Ziemlich ordentlich, oder?, Es stellt sich heraus, dass die Anzahl der Terme in Ihrem erweiterten Polynom immer eins mehr ist als die Leistung, die Sie erweitern. Das bedeutet, dass wir ein Polynom mit 4 Begriffen erstellen, da die Potenz in diesem Beispiel 3 ist.
Jeder Term hat eine (2x) und (-3) sowie die Formel „n wähle k“, wobei n=3. Sie können das 4 Mal aufschreiben, eines für jeden Term, wobei der k-Wert in „n choose k“ und die Potenzen für den Moment leer bleiben.
Als nächstes möchten Sie die k-Werte und Potenzen eingeben. Hier können Sie der Summationsformel folgen und die Potenz für jeden Term erhöhen., Aber es ist ziemlich einfach, nur den Mustern zu folgen.
Die k-Werte in“ n wählen k “ beginnen mit k=0 und erhöhen sich in jedem Term um 1. Der letzte Term sollte mit n gleich k enden, in diesem Fall n=3 und k=3.
Als nächstes müssen wir die Kräfte auf (2x) und (-3) hinzufügen.
Das Einschalten (2x) beginnt mit dem n-Wert, also in diesem Fall 3, und nimmt bei jedem Term um 1 ab, bis Sie auf Null kommen. Das Einschalten (-3) beginnt mit Null und erhöht sich jedes Mal um eins, bis Sie bei diesem Problem zu n oder 3 gelangen.,

Da jeder auf Null angehobene Wert gleich 1 ist, können Sie die Begriffe mit Potenzen von Null vereinfachen.

Als nächstes wenden Sie die Kräfte an und vereinfachen Sie sie, wo immer möglich.,

Die Pascal Dreieck Verknüpfung

Der letzte Teil besteht darin, die Kombinationsformel zu lösen. Der offensichtliche Weg, dies zu tun, besteht darin, die Kombinationsformel für jedes Problem anzuwenden. Aber wir werden hier eine nette kleine Abkürzung mit Pascals Dreieck nehmen.
Pascals Dreieck ist ein einfaches, aber mächtiges Dreieck, das durch Erstellen eines Dreiecks mit drei Einsen gebildet wird., Für jede Zeile danach schreiben Sie einfach 1 an beiden Enden und finden die mittlere Zahl (n), indem Sie die beiden Werte direkt darüber hinzufügen.

Jetzt ist hier der gute Teil. Versteckt in Pascals Dreieck sind alle Antworten auf jedes „n choose k“! Es ist wie ein geheimes kleines Cheatsheet!
Das folgende Diagramm zeigt Ihnen, wo sich die versteckten „n-k‘ s “ befinden.,

Für unser problem müssen wir lösen für: 3 wählen 0, 3 wählen 1, 3 wählen 2, und 3 wählen 3. Die alle Werte in der Zeile 4. Alles, was wir tun müssen, ist, in die 4.Reihe von Pascals Dreieck zu schauen und die Antworten abzugleichen.
Die 4. Zeile hat die Werte: 1, 3, 3, 1. Also werde ich nur in den Antworten für unsere n-k ersetzen.,

Schließlich müssen Sie nur jeden Begriff auf seine einfachste Form multiplizieren und vereinfachen. Vergessen Sie nicht, Ihre endgültige Antwort zu überprüfen, um sicherzustellen, dass die Kräfte für jeden Begriff immer noch zum Grad Ihres ursprünglichen Binoms beitragen! Vertrauen Sie mir, es ist unglaublich einfach, bei dieser Art von Problem einen Transkriptionsfehler zu machen 😉
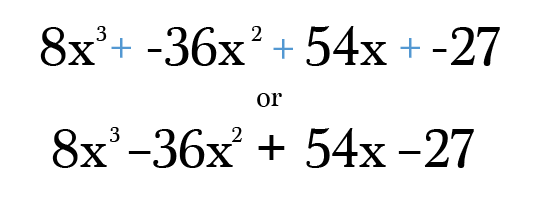
Benötigen Sie ein anderes Beispiel?,
Im obigen Video zeige ich Ihnen, wie Sie den Binomialsatz verwenden, um das Binom (x – 3y) ⁵ zu erweitern. Außerdem zeige ich Ihnen einige zusätzliche Tricks, um organisiert zu bleiben, und ein paar Schnellschecks, mit denen Sie häufige Fehler leicht identifizieren können.
Danke fürs Lesen!
❤ IN Verbindung BLEIBEN ❤
Bleiben Sie up-to-date mit allem, was Math Hacks ist up to!