Die Dirac-delta-Funktion ist eine Funktion eingeführt, im Jahr 1930 durch P. A. M. Dirac in seinem wegweisenden Buch über Quantenmechanik. Ein physikalisches Modell, das eine Delta-Funktion visualisiert, ist eine Massenverteilung der endlichen Gesamtmasse M—das Integral über die Massenverteilung., Wenn die Verteilung kleiner und kleiner wird, während M konstant ist, schrumpft die Massenverteilung zu einer Punktmasse, die per Definition Nullausdehnung hat und dennoch ein endliches Integral hat, das der Gesamtmasse M entspricht.In der Grenze einer Punktmasse wird die Verteilung zu einer Dirac-Delta-Funktion.
Heuristisch gesehen kann die Dirac-Delta-Funktion als Erweiterung des Kronecker-Deltas von integralen Indizes (Elemente von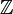 
) auf reale Indizes (Elemente von 
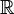) angesehen werden., Beachten Sie, dass das Kronecker Delta in einer Summierung als „Filter“ fungiert:
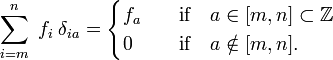
Analog dazu ist die Dirac delta Funktion δ(x−a) definiert durch (Ersetzen Sie i durch x und die Summation über i durch eine Integration über x),
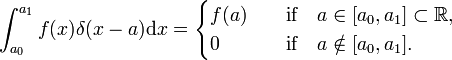
Die Dirac delta Funktion ist keine gewöhnliche gut erzogene map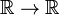 
, aber eine Verteilung, auch als unsachgemäße oder verallgemeinerte Funktion bekannt. Physiker drücken ihren besonderen Charakter aus, indem sie angeben, dass die Dirac-Delta-Funktion nur als Faktor in einem Integrand („unter dem Integral“) sinnvoll ist., Mathematiker sagen, dass die Delta-Funktion eine lineare Funktion auf einem Raum von Testfunktionen ist.
Inhalt
- 1 Eigenschaften
- 2 Delta-konvergente Sequenzen
- 2.1 Blockfunktionen
- 2.2 Gaußsche Funktionen
- 2.3 Lorentz-Cauchy-Funktionen
- 2.4 Sinc-Funktionen
- 3 Ableitungen der Delta-Funktion
- 3.,1 Eigenschaften der Ableitung
- 4 Primitiv
- 5 Die Dirac-Delta-Funktion in drei Dimensionen
- 6 Referenzen
Eigenschaften
Am häufigsten nimmt man die untere und die obere Grenze in der Definition der Delta-Funktion gleich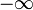 
bzw. 
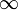. Von hier an wird dies geschehen.
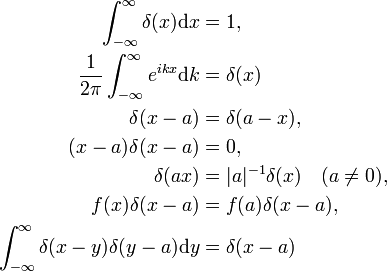
Der Nachweis dieser Eigenschaften des Physikers erfolgt durch ordnungsgemäße Substitutionen in das Integral und unter Verwendung der gewöhnlichen Regeln der Integralrechnung., Die Delta-Funktion als Fourier-Transformation der Einheitsfunktion f(x) = 1 (die zweite Eigenschaft) wird unten bewiesen. Die letzte Eigenschaft ist die Analogie der Multiplikation zweier Identitätsmatrizen,
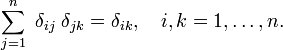
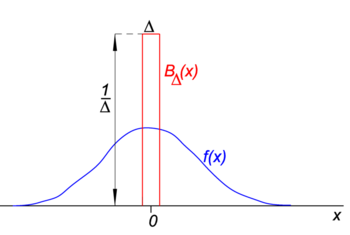
Abb. 1. Block („boxcar“) Funktion (rot) mal reguläre Funktion f (x) (blau).
Delta-konvergente Sequenzen
Es gibt Familien von regulären Funktionen Fa (x), von denen sich die Familienmitglieder durch den Wert eines einzelnen Parameters α unterscheiden., Ein Beispiel für eine solche Familie bildet die Familie der Gaußschen Funktionen Fa (x) = exp(−ax2), wobei die verschiedenen Werte des einzelnen Parameters α die verschiedenen Mitglieder unterscheiden. Wenn alle Mitglieder linear normalisierbar sind, dh das folgende Integral unabhängig von α endlich ist,
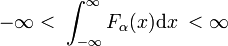
und alle Mitglieder um x = 0 spitzen, dann kann die Familie eine delta-konvergente Sequenz bilden.,
Blockfunktionen
Das einfachste Beispiel einer delta-konvergenten Sequenz wird durch die Familie der Blockfunktionen gebildet, gekennzeichnet durch positive Δ,
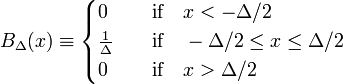
In Fig. 1 die Blockfunktion BΔ ist rot dargestellt. Offensichtlich ist die Fläche (Breite mal Höhe) unter der roten Kurve gleich unity, unabhängig vom Wert von Δ,
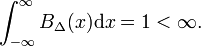
Lassen Sie die beliebige Funktion f(x) (blau in Fig. 1) sei kontinuierlich (keine Sprünge) und endlich in der Nähe von x=0., Wenn Δ sehr klein wird und die Blockfunktion sehr schmal ist (und notwendigerweise sehr hoch, weil Breite mal Höhe konstant ist), wird das Produkt f(x) BΔ(x) in guter Näherung gleich f(0) BΔ(x). Je schmaler der block, desto besser die Annäherung., Für Δ, das auf Null geht,
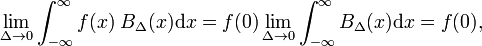
, das mit der Definition der Delta-Funktion verglichen werden kann,
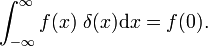
Dies zeigt, dass die Familie der Blockfunktionen zur Dirac-Delta-Funktion konvergiert, um den Parameter Δ zu verringern; Die Familie bildet eine delta-konvergente Sequenz:
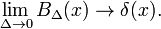
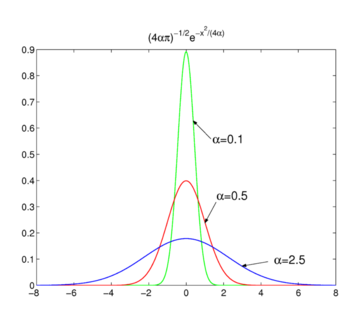
Abb. 2. Gaußsche Funktionen.
Hinweis: Wir haben über die gesamte reale Achse integriert., Offensichtlich ist dies nicht notwendig, wir hätten die nullwertigen Flügel der Blockfunktion ausschließen und nur über den Buckel in der Mitte integrieren können, von −Δ/2 bis +Δ/2. In mathematischen Texten, wie z.B. Ref. , diese Verfeinerung in den Integrationsgrenzen ist in der Definition der delta-konvergenten Sequenz enthalten. Das heißt, es ist erforderlich, dass die Integrale über den beiden Flügeln in der Grenze verschwinden. Da die delta-konvergenten Sequenzen, die in physikalischen Anwendungen auftreten, normalerweise diese Bedingung erfüllen, lassen wir die genauere mathematische Definition weg.,
Gaußsche Funktionen
Betrachten Sie die Familie,
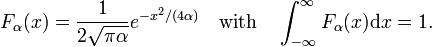
Wie in Abb. 2 die Funktionen Peak um x = 0 und werden schmaler für abnehmende α. Damit die Familie der Gauß-Funktionen bildet ein delta-konvergente Sequenz,
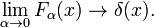
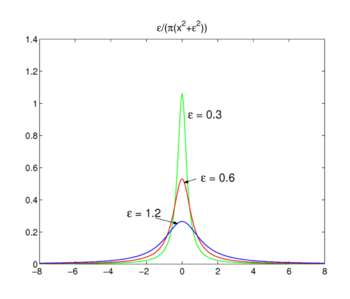
Abb. 3. Lorentz – Cauchy-Funktionen
Lorentz-Cauchy-Funktionen
Die in Abb., 3
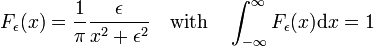
forms a delta-convergent sequence,
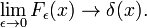
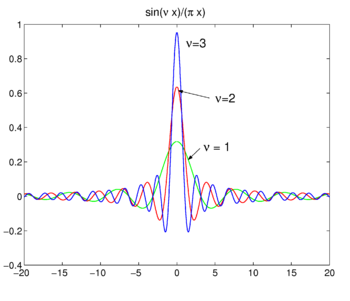
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 ist
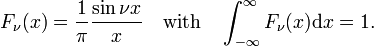
Diese Familie konvergiert zur Delta-Funktion zur Erhöhung von ν
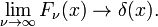
Diese Grenze führt leicht zur Fourier-Integraldarstellung der Delta-Funktion:
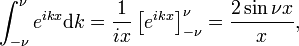
so dass
iv Die Dirac-Delta-Funktion ist die Fourier-Transformation der Einheitsfunktion f(x) = 1.
Ableitungen der Delta-Funktion
Betrachten Sie eine differenzierbare Funktion f (x), die bei plus und minus unendlich verschwindet.,d=“ed7dae11d6″>
Auf die gleiche Weise, wie man die Fluktuationsregel und Hermitizität des quantenmechanischen Impulsoperators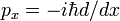 
beweist, haben wir hier gezeigt, dass d/dx anti-hermitisch ist,
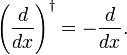
Wenn wir das Integral als inneres Produkt schreiben, folgt es aus der partiellen Integration und dem Verschwinden von f(x) an den Integrationsgrenzen, dass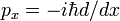/p>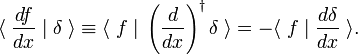
Diese Umsatzregel wird als Definition der Ableitung der Delta-Funktion verwendet,
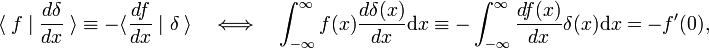
wobei die Primzahl die erste Ableitung von f(x) angibt., Gemäß der Definition der Delta-Funktion wird die erste Ableitung in x = 0 ausgewertet. Unter Verwendung der m-fachen Umsatzregel folgt, dass die m −te Ableitung der Delta-Funktion durch
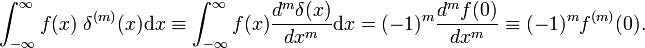
Eigenschaften der Ableitung
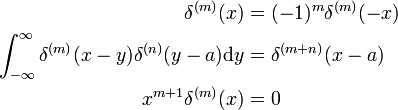
Diese Ergebnisse können durch die Substitution x → – x und die Verwendung der Umsatzregel für d/dx (siehe oben) nachgewiesen werden.,
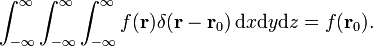
Die dreidimensionale delta funktion kann faktorisiert werden
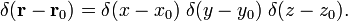
In sphärischen polarkoordinaten
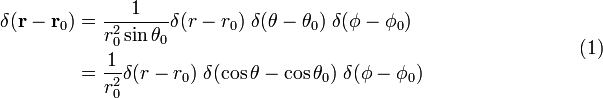
Proof of equation (1)
Write
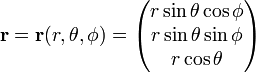
Jacobian (Jacobi-Determinante) dieser Transformation von kartesischen Koordinaten zu sphärischen Polarkoordinaten ist
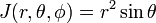
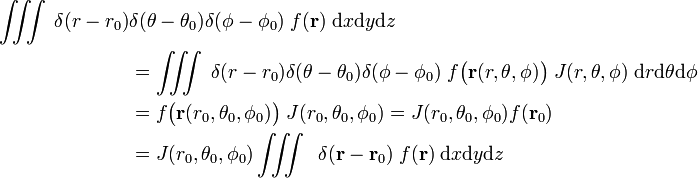
so dass
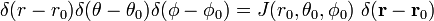
und
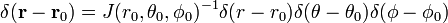
Die letzte Zeile in der Gleichung (1) folgt aus der Kettenregel.,
Die folgende nützliche und häufig angewandte Eigenschaft ist hier bewiesen,
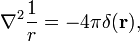
wobei ∇2 der Laplace-Operator in dreidimensionalen kartesischen Koordinaten ist und r die Länge von r.