Der“ Einheitskreis “ ist ein Kreis mit einem Radius von 1.
Da es so einfach ist, ist es eine großartige Möglichkeit, Längen und Winkel zu lernen und darüber zu sprechen.
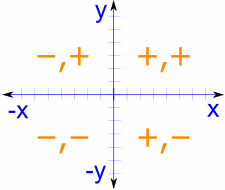
Die Mitte wird auf einen Graphen gelegt, in dem sich die x-Achse und die y-Achse kreuzen, so dass wir hier diese ordentliche Anordnung erhalten.
Sinus, Kosinus und Tangens
Da der Radius 1 ist, können wir Sinus, Kosinus und Tangens direkt messen.,
Was passiert, wenn der Winkel, θ, 0°?
cos 0° = 1, sin 0° = 0 und tan 0° = 0
Was passiert, wenn θ = 90°?
cos 90° = 0, sin 90° = 1 und tan von 90° ist nicht definiert
Probieren Sie Es Selbst!
Versuchen Sie es!, Bewegen Sie die Maus, um zu sehen, wie verschiedene Winkel (in Bogenmaß oder Grad) Sinus, Kosinus und Tangente beeinflussen
Die“ Seiten “ können nach den Regeln der kartesischen Koordinaten positiv oder negativ sein. Dies macht den Sinus, Kosinus und Tangente Wechsel zwischen positiven und negativen Werten auch.
Versuchen Sie auch die interaktive Einheit Kreis.,
Pythagoras
Der Satz von Pythagoras besagt, dass für ein rechtwinkliges Dreieck das Quadrat der langen Seite der Summe der Quadrate der anderen beiden Seiten entspricht:
x2 + y2 = 12
Aber 12 ist nur 1, also:
x2 + y2 = 1
(die Gleichung des Einheitskreises)
Da x=cos und y=sin ist, erhalten wir:
(cos(θ))2 + (sin(θ))2 = 1
eine nützliche „Identität“
Wichtige Winkel: 30°, 45° und 60°
Sie sollten versuchen, denken Sie an sin, cos und tan für die Winkel 30°, 45° und 60°.,
Ja, ja, es ist ein Schmerz, sich an Dinge erinnern zu müssen, aber es wird das Leben erleichtern, wenn Sie sie kennen, nicht nur in Prüfungen, sondern auch in anderen Zeiten, in denen Sie schnelle Schätzungen vornehmen müssen usw.
Dies sind die Werte, die Sie sich merken sollten!,id=“0f47f3223b“>
What about tan?,
Nun, tan = sin / cos, also können wir es so berechnen:
tan (30°) =sin (30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan (45°) =sin (45°)cos(45°) = √2/2√2/2 = 1
tan (60°) =sin (60°)cos(60°) = √3/21/2 = √3
* Hinweis: Das Schreiben von 1√3 kann Markierungen kosten (siehe rationale Nenner), verwenden Sie stattdessen √33
Quick Sketch
Eine andere Möglichkeit, sich an 30° und 60° zu erinnern, besteht darin, eine schnelle Skizze zu erstellen:
| Zeichnen Sie ein Dreieck mit Seitenlängen von 2 | 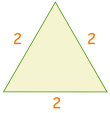 |
|
Halbieren.,div id=“56c966b492″> Beispiel: sin(30°)Sinus: sohcahtoa Sinus ist gegenüber geteilt durch hypotenuse
sin(30°) = oppositehypotenuse = 12
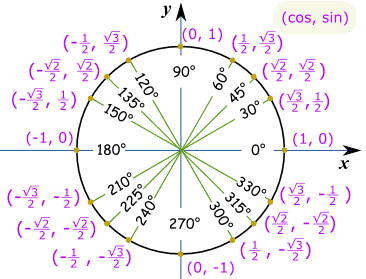
Der ganze KreisFür den ganzen Kreis benötigen wir Werte in jedem Quadranten mit dem richtigen Plus-oder Minuszeichen gemäß kartesischen Koordinaten: Beachten Sie, dass cos der erste und sin der zweite ist (cos, sin):
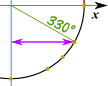
Als PDF speichern Beispiel: Was ist cos(330°) ?,
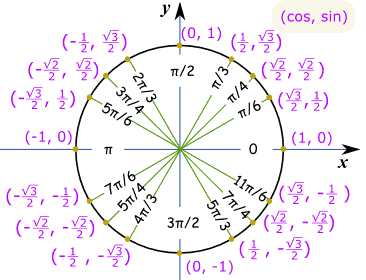
Machen sie eine skizze wie diese, und wir können sehen, es ist die“ lange “ wert: √32 Und dies ist die gleiche Einheit Kreis in radiant.
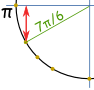
Beispiel: Was ist sin(7π/6) ?
Denken Sie „7π/6 = π + π/6“, dann machen eine Skizze. Wir können dann sehen, dass es negativ ist und der“ kurze “ Wert ist: – ½ |