La «Unidad» el Círculo es un círculo con un radio de 1.
siendo tan simple, es una gran manera de aprender y hablar sobre longitudes y ángulos.
el centro se pone en un gráfico donde el eje x y el eje y se cruzan, por lo que obtenemos esta disposición ordenada aquí.
seno, coseno y tangente
debido a que el radio es 1, podemos medir directamente seno, coseno y tangente.,
¿Qué sucede cuando el ángulo θ, es de 0°?
cos 0° = 1, el pecado de 0° = 0 y bronceado 0° = 0
¿Qué sucede cuando θ es de 90°?
cos 90° = 0, sin 90° = 1 y tan 90° es indefinido
¡pruébalo tú mismo!
¡inténtalo!, Mueva el ratón para ver cómo diferentes ángulos (en radianes o grados) afectan seno, coseno y tangente
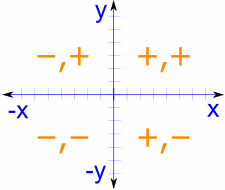
los «lados» pueden ser positivos o negativos de acuerdo con las reglas de coordenadas cartesianas. Esto hace que el seno, coseno y tangente cambio entre valores positivos y negativos también.
también Pruebe el círculo de unidad interactiva.,
Pitágoras
El teorema de Pitágoras dice que para un triángulo en ángulo recto, el cuadrado del lado largo es igual a la suma de los cuadrados de los otros dos sides:
x2 + y2 = 12
but 12 is just 1, so:
x2 + y2 = 1
(the equation of the unit circle)
also, since x=cos and Y=Sin, we get:
(COS(θ))2 + (Sin(θ))2 = 1
a useful «identity»
important angles: 30°, 45° y 60°
debe tratar de recordar sin, cos y tan para los ángulos 30°, 45° y 60°.,
sí, sí, es un dolor tener que recordar cosas, pero te hará la vida más fácil cuando las conozcas, no solo en los exámenes, sino en otras ocasiones cuando necesites hacer estimaciones rápidas, etc.
¡Estos son los valores que debes recordar!,id=»0f47f3223b»>
What about tan?,
bueno, tan = sin / cos, así que podemos calcularlo así:
tan(30°) = sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan (45°) = sin (45°)cos(45°) = √2/2√2/2 = 1
tan (60°) = sin (60°)cos(60°) = √3/21/2 = √3
* Nota: escribir 1√3 puede costarle marcas (consulte denominadores racionales), por lo que en su lugar use √33
Quick Sketch
otra forma de ayudarlo a recordar 30° y 60° es hacer un sketch rápido:
| dibujar un triángulo con longitudes laterales de 2 | |
|
cortar por la mitad.,div id=»56c966b492″> ejemplo: sin(30°)Sine: sohcahtoa sine is opposite divided by hypotenuse
sin(30°) = oppositehypotenuse = 12
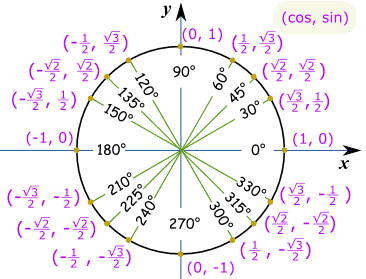
todo el círculopara todo el círculo necesitamos valores en cada cuadrante, con el signo más o menos correcto según las coordenadas cartesianas: tenga en cuenta que Cos es primero y sin es segundo, por lo que va (cos, sin):
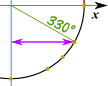
Guardar como PDF ejemplo: ¿Qué es cos(330°) ?,
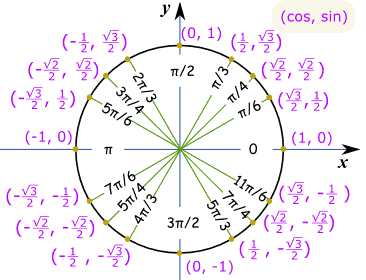
Hacer un dibujo como este, y podemos ver que es el «largo» valor»: √32 Y este es el mismo Círculo Unidad en radianes.
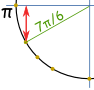
ejemplo: ¿Qué es sin(7π / 6) ?
piense en «7π/6 = π + π / 6», luego haga un boceto. entonces podemos ver que es negativo y es el valor «corto»: – ½ Articles |