Contenido – aceleración Constante

Contenido

aceleración Constante

todos Estamos familiarizados con el hecho de que un coche se acelera cuando ponemos nuestro pie en el acelerador. La velocidad de cambio de la velocidad de una partícula con respecto al tiempo se llama su aceleración. Si la velocidad de la partícula cambia a una velocidad constante, entonces esta velocidad se llama aceleración constante.,

por ejemplo, si la velocidad de una partícula que se mueve en línea recta cambia uniformemente (a una velocidad de cambio constante) de 2 m/s a 5 m/s durante un segundo, entonces su aceleración constante es de 3 m/s\(^2\).

velocidad decreciente

si una partícula tiene una velocidad inicial de 6 m/s y una aceleración constante de \(-2\) m/s\(^2\), entonces:

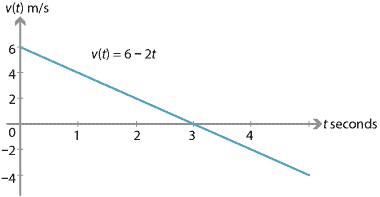
durante los primeros tres segundos, la velocidad de la partícula está disminuyendo (la partícula está ralentizando). A los tres segundos, la partícula está momentáneamente en reposo., Después de tres segundos, la velocidad sigue disminuyendo, pero la velocidad está aumentando (la partícula va más y más rápido).

Resumen

Si asumimos que la tasa de cambio de velocidad (aceleración) es una constante, la constante de aceleración está dada por

\

Más precisamente, la aceleración constante \(a\) es dado por la fórmula

\

donde \(v(t_i)\) es la velocidad en el tiempo \(t_i\). Dado que la velocidad es un vector, también lo es la aceleración.,

las fórmulas de aceleración constante para el movimiento en línea recta

a lo largo de esta sección, hemos estado considerando el movimiento en línea recta con aceleración constante. Esta situación es muy común; por ejemplo, un cuerpo que se mueve bajo la influencia de la gravedad viaja con una aceleración constante.

se supone que el movimiento comienza cuando \(t = 0\), y que la posición inicial se toma como el origen, es decir, \(x(0) = 0\).,

Las cinco ecuaciones de movimiento

1. \(v = u + a\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}a^2\)
4. \(v^2 = u^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}a^2\)

tenga en cuenta. Cada una de las cinco ecuaciones involucra cuatro de las cinco variables \(u, v, x, A, t\). Si se conocen los valores de tres de las variables, entonces los valores restantes se pueden encontrar usando dos de las ecuaciones.,

derivando las fórmulas de aceleración constante

la primera ecuación de movimiento

dado que la aceleración es constante, tenemos \(a = \dfrac{v-u}{t}\). Esto da la primera ecuación de movimiento, \(v = u + at\).

la segunda ecuación de movimiento

la segunda ecuación,

\

dice que el desplazamiento se obtiene multiplicando el promedio de las velocidades inicial y final por el tiempo transcurrido durante el movimiento. Más simplemente:

\

podemos derivar esta ecuación usando el hecho de que el desplazamiento es igual al área con signos bajo el gráfico velocidad–tiempo.,

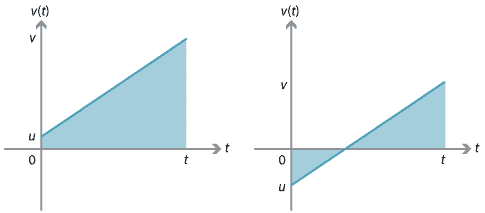
para el gráfico de la derecha, el desplazamiento se puede encontrar considerando los dos triángulos entre el gráfico y el eje \(t\). Uno de los triángulos tiene un área con signo positivo y el otro tiene un área con signo negativo.

Encontrar el desplazamiento de una partícula desde el gráfico velocidad–tiempo usando la integración se discutirá en una sección posterior de este módulo.,

La tercera ecuación de movimiento

la Sustitución de \(v\) de la primera ecuación en la segunda ecuación nos da

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+a)t}{2} \\ &= \dfrac{2ut+a^2}{2} \\ &= ut + \dfrac{1}{2}a^2, \end{align*}

que es la tercera ecuación. Por lo tanto \(x\) es una cuadrática en \(t\), y por lo tanto el gráfico de \(x\) contra \(t\) es una parábola.

la cuarta ecuación de movimiento

de la primera ecuación, tenemos \(t = \dfrac{v-u} {a}\)., Sustituyendo esto en la segunda ecuación nos da

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{align*}

reordenando para hacer \(v^2\) el sujeto produce la cuarta ecuación: \(v^2 = U^2 + 2AX\).

la quinta ecuación de movimiento

de la primera ecuación, tenemos \(u = v-at\)., Usando la segunda ecuación, obtenemos

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-a+v)t}{2} \\ &= \dfrac{2vt-a^2}{2} \\ &= vt-\dfrac{1}{2}a^2, \end{align*}

que es la quinta parte de la ecuación.

movimiento Vertical

El movimiento debido a la gravedad es un buen contexto en el que demostrar el uso de las fórmulas de aceleración constante., Como se discutió anteriormente, nuestras dos direcciones en movimiento vertical son hacia arriba y hacia abajo, y se tiene que tomar una decisión en cuanto a cuál de las dos direcciones es positiva. La aceleración debida a la gravedad es una constante, con magnitud denotada por \(g\). En el siguiente ejemplo, tomamos la dirección hacia arriba para ser positiva y tomamos \(g = 10\) m/s\(^2\).

uso adicional de las ecuaciones de movimiento

Next page – Content – Average velocity and average speed