autómatas Finitos puede tener resultados correspondientes a cada transición. Hay dos tipos de máquinas de estado finito que generan salida –
- Mealy Machine
- Moore machine
Mealy Machine
Una máquina harinosa es un FSM cuya salida depende del estado actual, así como de la entrada presente.,
Puede ser descrito por una tupla 6 (Q, ∑, o, δ, X, q0) donde −
-
Q es un conjunto finito de Estados.
-
∑ es un conjunto finito de símbolos llamado alfabeto de entrada.
-
O es un conjunto finito de símbolos llamado alfabeto de salida.
-
δ es la función de transición de entrada donde δ: Q × ∑ → Q
-
X es la función de transición de salida donde X: Q × ∑ → O
-
q0 es el estado inicial desde donde se procesa cualquier entrada (q0 ∈ Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
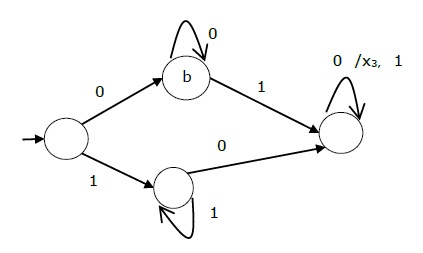
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
una máquina de Moore puede ser descrita por una tupla 6 (Q, ∑, o, δ, X, q0) donde −
-
Q es un conjunto finito de Estados.
-
∑ es un conjunto finito de símbolos llamado alfabeto de entrada.
-
O es un conjunto finito de símbolos llamado alfabeto de salida.
-
δ es la función de transición de entrada donde δ: Q × ∑ → Q
-
X es la función de transición de salida donde X: Q → O
-
q0 es el estado inicial desde donde se procesa cualquier entrada (q0 ∈ Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
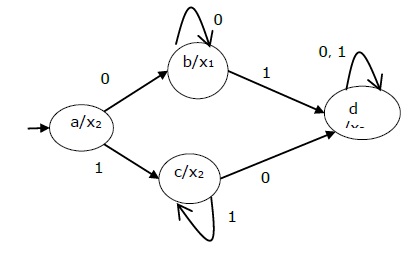
Mealy Machine vs., Máquina Moore
la siguiente tabla destaca los puntos que diferencian una máquina harinosa de una máquina Moore.
Mealy Machine Moore Machine la salida depende tanto del estado actual como de la entrada presente la salida depende solo del estado actual. generalmente, tiene menos estados que la máquina de Moore. generalmente, tiene más estados que la máquina harinosa., el valor de la función output es una función de las transiciones y los cambios, cuando se realiza la lógica de entrada en el estado actual. el valor de la función de salida es una función del estado actual y de los cambios en los bordes del reloj, siempre que se produzcan cambios de estado. las máquinas harinosas reaccionan más rápido a las entradas. Generalmente reaccionan en el mismo ciclo de reloj. en las máquinas Moore, se requiere más lógica para decodificar las salidas, lo que resulta en más retrasos de circuito. Generalmente reaccionan un ciclo de reloj más tarde., Moore Machine to Mealy Machine
Algorithm 4
Input − Moore Machine
Output − Mealy Machine
Paso 1 − tome un formato de tabla de transición de máquina harinosa en blanco.
Paso 2-copie todos los estados de transición de la máquina Moore en este formato de tabla.
Paso 3-Compruebe los estados actuales y sus salidas correspondientes en la tabla de Estado de la máquina Moore; si para un estado la salida Qi es m, cópiela en las columnas de salida de la tabla de estado de la máquina harinosa donde aparece Qi en el siguiente estado.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
Paso 2 – si todas las salidas de Qi son iguales, copia el estado Qi. Si tiene N salidas distintas, romper Qi en n estados como Qin donde n = 0, 1, 2…….
Paso 3 – si la salida del estado inicial es 1, Inserte un nuevo estado inicial al principio que da salida 0.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Pero los Estados ‘ b ‘y’ c ‘ producen salidas diferentes (1 y 0). Por lo tanto, dividimos b en b0, b1 y c En c0, c1.,»>
Output