heurísticamente, la función delta de Dirac puede verse como una extensión del delta de Kronecker desde índices integrales (elementos de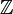 
) a índices reales (elementos de 
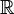)., Tenga en cuenta que el delta de Kronecker actúa como un «filtro» en una suma:
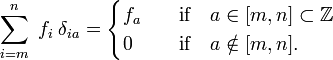
en analogía, la función delta de Dirac δ(x−a) se define por (reemplazar I por x y la suma sobre i por una integración sobre x),
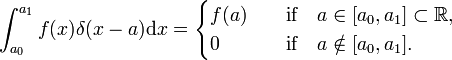
La función delta de Dirac no es map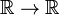 
, pero una distribución, también conocida como función incorrecta o generalizada. Los físicos expresan su carácter especial afirmando que la función delta de Dirac solo tiene sentido como un factor en un integrando («bajo la integral»)., Los matemáticos dicen que la función delta es una función lineal en un espacio de funciones de prueba.
Contenido
- 1 Propiedades
- 2 Delta-secuencias convergentes
- 2.1 Bloque de funciones
- 2.2 Gauss funciones
- 2.3 Lorentz-Cauchy funciones
- 2.4 Sinc funciones
- 3 Derivados de la función delta
- 3.,1 propiedades de la derivada
- 4 Primitiva
- 5 La función delta de Dirac en tres dimensiones
- 6 Referencias
propiedades
más comúnmente se toma el límite inferior y superior en la definición de la función delta igual a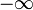 
y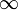 
, respectivamente. De aquí en adelante esto se hará.
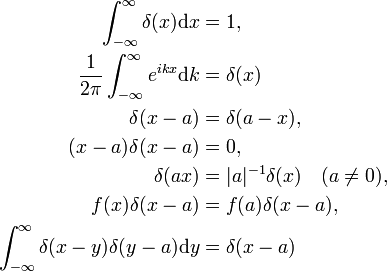
la prueba del físico de estas propiedades procede haciendo sustituciones adecuadas en la integral y utilizando las reglas ordinarias del cálculo integral., La función delta como transformada de Fourier de la función unitaria f(x) = 1 (la segunda propiedad) se probará a continuación. La última propiedad es la analogía de la multiplicación de dos matrices de identidad,
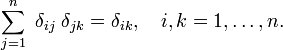
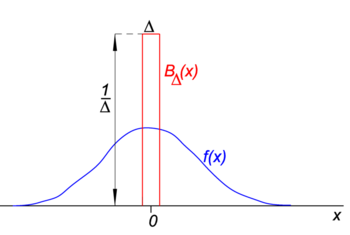
Fig. 1. Función de bloque («boxcar») (rojo) veces función regular f (x) (azul).
Delta-secuencias convergentes
existen familias de funciones regulares Fa (x) de las cuales los miembros de la familia difieren por el valor de un único parámetro α., Un ejemplo de tal familia está formado por la familia de funciones gaussianas Fa(x) = exp(−ax2), donde los diferentes valores del único parámetro α distinguen los diferentes miembros. Cuando todos los miembros son linealmente normalizables, es decir, la siguiente integral es finita independientemente de α,
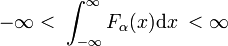
y todos los miembros alcanzan un pico alrededor de x = 0, entonces la familia puede formar una secuencia delta-convergente.,
funciones de bloque
el ejemplo más simple de una secuencia delta-convergente está formado por la familia de funciones de bloque, caracterizada por Δ positivo,
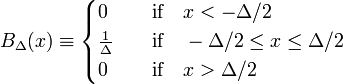
en la Fig. 1 la función de bloque BΔ se muestra en rojo. Evidentemente, el área (ancho por alto) bajo la curva roja es igual a la unidad, independientemente del valor de Δ,
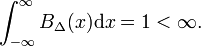
deje la función arbitraria f(x) (azul en la Fig. 1) ser continuo (sin saltos) y finito en la vecindad de x=0., Cuando Δ se vuelve muy pequeño, y la función de bloque muy estrecha (y necesariamente muy alta porque la anchura por la altura es constante) el producto f(x) BΔ(x) se vuelve en buena aproximación igual a f(0) BΔ(x). Cuanto más estrecho sea el bloque, mejor será la aproximación., Por lo tanto para Δ va a cero,
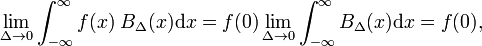
que pueden ser comparados con la definición de la función delta,
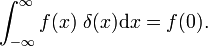
Esto muestra que la familia de bloque de funciones converge a la función delta de Dirac para disminuir el parámetro Δ; la familia forma un delta-convergente secuencia:
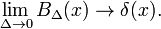
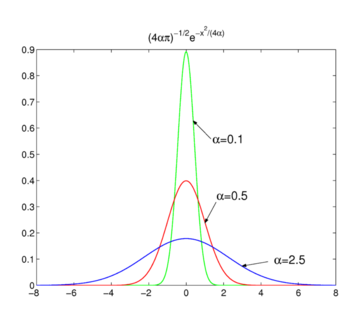
Fig. 2. Funciones gaussianas.
Nota: integramos todo el eje real., Obviamente esto no es necesario, podríamos haber excluido las alas de valor cero de la función de bloque e integrado solo sobre la joroba en el medio, de −Δ/2 a +Δ/2. In mathematical texts, as E.G. Ref. , este refinamiento en los límites de integración se incluye en la definición de la secuencia delta-convergente. Es decir, se requiere que las integrales sobre las dos alas desaparezcan en el límite. Debido a que las secuencias delta-convergentes encontradas en aplicaciones físicas generalmente satisfacen esta condición, omitimos la definición matemática más exacta.,
Gaussian funciones
Considere la familia,
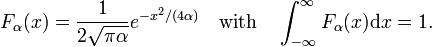
Como se muestra en la Fig. 2 las funciones alcanzan su pico alrededor de x = 0 y se vuelven más estrechas para disminuir α. Por lo tanto la familia de Gauss funciones de forma un delta-convergente de la secuencia,
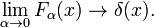
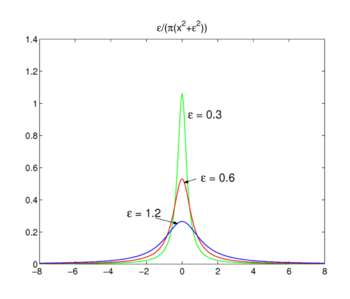
Fig. 3. Lorentz-Cauchy funciones
Lorentz-Cauchy funciones
La familia de funciones que se muestra en la Fig., 3
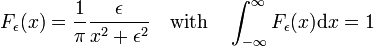
forms a delta-convergent sequence,
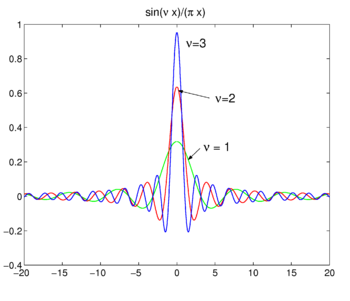
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 es
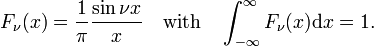
Esta familia converge a la función delta para aumentar ν
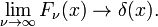
Este límite conduce fácilmente a la representación integral de Fourier de la función delta:
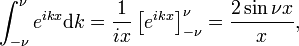
para que
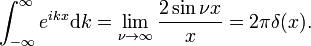
La función delta de Dirac es la transformada de Fourier de la unidad de la función f(x) = 1.
las derivadas de la función delta
consideran una función diferenciable f(x) que desaparece en más y menos infinito.,d=»ed7dae11d6″>
de la misma manera que se demuestra la regla de rotación y Hermiticidad del operador de momento mecánico cuántico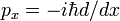 
, mostramos aquí que d/dx es anti-Hermitian,
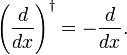
de hecho, cuando escribimos la integral como un producto interno, se sigue de la integración parcial y la desaparición de F(X) en los límites de integración que
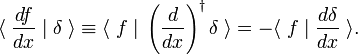
esta regla de rotación se utiliza como la definición de la derivada de la función delta,
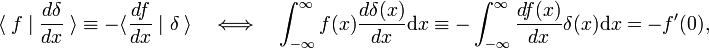
donde el primo indica la primera derivada de f(x)., De acuerdo con la definición de la función delta, la primera derivada se evalúa en x = 0. Usando m veces La regla de rotación, se deduce que la derivada m-ésima de la función delta está definida por
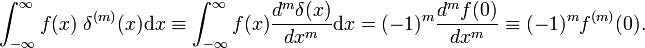
propiedades de la derivada
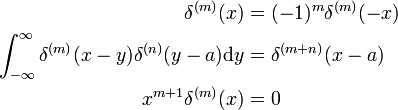
estos resultados se pueden probar haciendo la sustitución x → −x y el uso de la regla de rotación para d / dx (ver arriba).,
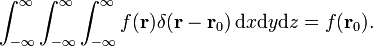
Las tres dimensiones de función delta pueden ser factorizados
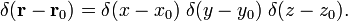
esféricas En coordenadas polares
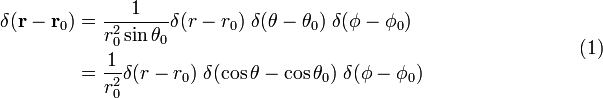
Prueba de la ecuación (1)
Escribir
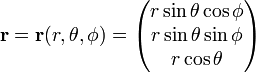
El Jacobiano (Jacobi determinante) de esta transformación de coordenadas Cartesianas a esféricas en coordenadas polares es
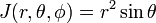
Considere
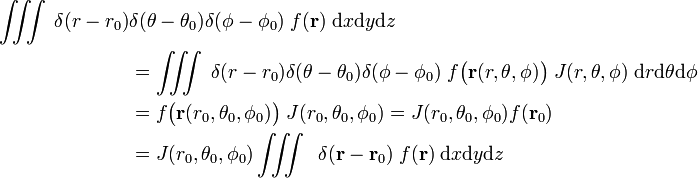
para que
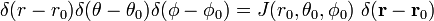
y
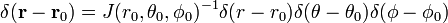
La última línea en la ecuación (1) se sigue de la regla de la cadena.,
La siguiente propiedad útil y frecuentemente aplicada se prueba aquí,
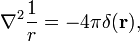
donde ∇2 es el operador de Laplace en coordenadas cartesianas tridimensionales y r es la longitud de r.