comencemos con un ejemplo sencillo, digamos que queremos multiplicar (2x-3)3. Esto no sería demasiado difícil de hacer mano larga, pero vamos a utilizar el teorema binomial para que cuando te encuentras con expansiones más grandes, tales como binomios elevados a los poderes 4, 5, 6, … usted sabrá exactamente qué hacer.
para comenzar, debe identificar los dos términos de su binomio (las posiciones x E y de nuestra fórmula anterior) y la potencia (n) A la que está expandiendo el binomio.,
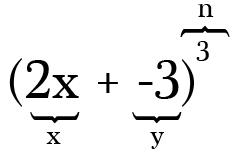
por ejemplo, Para expandir (2x-3)3, los dos términos son 2x -3 y el poder, o el valor de n es 3. Tenga en cuenta que cada vez que usted tiene una resta en su binomio es oh tan importante recordar incluir el menos como un símbolo negativo en el término acompañante.
lo maravilloso del teorema del binomio es que nos permite encontrar el polinomio expandido sin multiplicar un montón de binomios juntos. Bastante limpio, ¿verdad?, Resulta que el número de términos en su polinomio expandido siempre será uno más que el poder que está expandiendo. Eso significa que vamos a crear un polinomio con 4 Términos ya que la potencia en este ejemplo es 3.
cada término tendrá a (2x) y (-3), así como la fórmula «N elige k» donde n=3. Puedes seguir adelante y escribirlo 4 veces, una para cada término, dejando el valor k en «n elige k» y los poderes en blanco por el momento.
a continuación, querrá completar los valores k y poderes. Aquí puede seguir la fórmula de suma, aumentando la potencia para cada término., Pero es bastante fácil simplemente seguir los patrones.
los valores de k en «n choose k», comenzarán con k=0 y aumentarán en 1 en cada término. El último término debe terminar con n igual a k, en este caso n=3 y k=3.
a continuación tenemos que añadir los poderes sobre (2x) y (-3).
el encendido (2x) comenzará con el valor n, por lo que en este caso 3, y disminuirá en 1 en cada término, hasta llegar a cero. El encendido (-3) comenzará con cero y aumentará en uno cada vez hasta que llegue a n, o 3 en este problema.,

Debido a que cualquier valor elevado a la potencia cero es igual a 1, se pueden simplificar los términos con potencias de cero.

después de pasar por delante y aplicar los poderes y simplificar siempre que sea posible.,

El Triángulo de Pascal de acceso directo

La última parte es la de resolver las combinaciones de la fórmula. La forma obvia de hacer esto es aplicar la fórmula de combinaciones para cada problema. Pero vamos a tomar un pequeño atajo aquí usando el Triángulo de Pascal.
El Triángulo de Pascal es un triángulo simple, pero poderoso formado creando un triángulo con tres 1 Para comenzar., Para cada fila a partir de entonces, simplemente escriba 1 en ambos extremos, y encuentre el(los) Número (s) del medio agregando los dos valores directamente arriba.

Ahora aquí está la parte buena. ¡Escondidas dentro del Triángulo de Pascal están todas las respuestas a cualquier «N choose k»! Es como un secreto pequeño cheatsheet!
el siguiente diagrama le muestra dónde se encuentran las «n choose k» ocultas.,

Para nuestro problema que debemos resolver para: 3 seleccione 0, 3 elija 1, 3 elija 2, y 3 elija 3. Que son todos los valores en la 4ª fila. Así que todo lo que necesitamos hacer es mirar a la 4ª fila del Triángulo de Pascal y hacer coincidir las respuestas.
La 4ª fila tiene los valores: 1, 3, 3, 1. Así que voy a sustituir en las respuestas para nuestro n elegir k.,

por último, todo lo que necesitas hacer es multiplicar y simplificar cada término es la forma más sencilla. No se olvide de comprobar su respuesta final para asegurarse de que los poderes en cada término todavía añadir al grado de su binomio original! Confía en mí, es muy fácil cometer un error de transcripción en este tipo de problema 😉
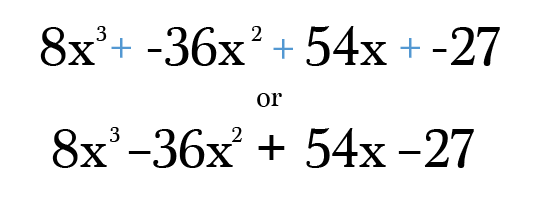
Necesita otro ejemplo?,
en el video de arriba, te muestro cómo usar el teorema Binomial para expandir el binomio (x – 3y)⁵. Además, te muestro algunos trucos adicionales para mantenerte organizado y un par de comprobaciones rápidas que puedes usar para identificar fácilmente errores comunes.
Gracias por leer!
❤ manténgase conectado ❤
¡Manténgase al día con todo lo que Math Hacks está haciendo!