Las funciones logarítmicas son las inversas de las funciones exponenciales. La inversa de la función exponencial y = ax es x = ay. La función logarítmica y = logax se define como equivalente a la ecuación exponencial x = ay. y = logax solo bajo las siguientes condiciones: x = ay, a > 0, y a≠1. Se llama la función logarítmica con base a.
considere lo que significa la inversa de la función exponencial: x = ay., Dado un número x y una base a, ¿a qué potencia y debe elevarse a igual a x? Este exponente desconocido, y, es igual a logax. Así que ves un logaritmo no es más que un exponente. Por definición, alogax = x, para cada real x > 0.
a Continuación se muestran los gráficos de la forma y = logax cuando un > 1 y cuando 0 < < 1. Observe que el dominio consiste solo en los números reales positivos, y que la función siempre aumenta a medida que aumenta x.,
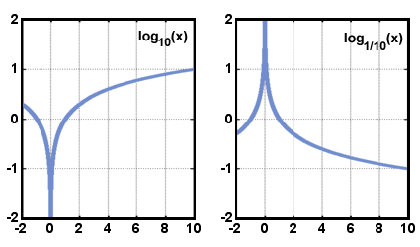
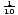 x.
x.el dominio de una función logarítmica es números reales mayores que cero, y el rango Es números reales. El gráfico de y = logax es simétrico al gráfico de y = ax con respecto a la línea y = x. esta relación es verdadera para cualquier función y su inversa.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(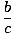 ) = logab – logac., ) = logab – logac., |
| su sistema loga(xd) = d logax |
natural de la función logarítmica es una función logarítmica con base e. f (x) = logex = ln x, donde x > 0. ln x es solo una nueva forma de notación para logaritmos con base e. la mayoría de las calculadoras tienen botones etiquetados » log » y «ln». El botón» log «asume que la base es diez, y el botón» ln», por supuesto, permite que la base sea igual a e., La función logarítmica con base 10 a veces se llama función logarítmica común. Se usa ampliamente porque nuestro sistema de numeración tiene una base de diez. Los logaritmos naturales se ven más a menudo en el cálculo.
Existen dos fórmulas que permiten cambiar la base de una función logarítmica. El primero dice esto: logab = 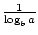 . La fórmula más famosa y útil para cambiar bases se llama comúnmente el cambio de Fórmula Base. Permite que la base de una función logarítmica sea cambiada a cualquier número real positivo ≠1. Indica que logax =
. La fórmula más famosa y útil para cambiar bases se llama comúnmente el cambio de Fórmula Base. Permite que la base de una función logarítmica sea cambiada a cualquier número real positivo ≠1. Indica que logax = 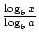 ., En este caso, a, b y x son todos números reales positivos y a, b≠1.
., En este caso, a, b y x son todos números reales positivos y a, b≠1.
en la siguiente sección, discutiremos algunas aplicaciones de funciones exponenciales y logarítmicas.