en estas páginas nos fijamos en algunos conceptos interesantes, nos fijamos en el espacio curvo: lo que significa el espacio curvo, cómo podemos saber si un espacio está curvado desde dentro o desde fuera de él.
observamos cómo podemos incrustar en el tipo de espacio dentro de otro y vemos que podemos mapear entre diferentes espacios de diferentes maneras.
también nos fijamos en la compactación y cómo podemos representar vectores infinitamente grandes e infinitesimalmente pequeños en nuestros espacios de maneras que no conducen a singularidades y otros problemas.,
estos conceptos resultan útiles, incluso cuando estamos trabajando con espacio plano, encontraremos formas de representar vectores y planos que no pasan por el origen. Esto nos da formas de representar rotaciones y traducciones como una sola operación.
La otra aplicación es el espacio-tiempo relativista.
Geometría Rienmanniana
en Geometría rienmanniana el espacio puede curvarse en diferentes lugares (ver colectores) aquí nos fijamos en geometrías donde la curva del espacio es constante.,
Geometría Eulidiana
espacio plano
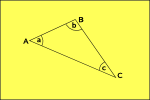
geometría hiperbólica
curvas de espacio hacia afuera
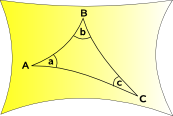
geometría esférica y geometría elíptica
curvas de espacio hacia adentro
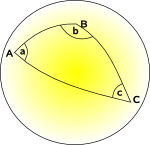
en una geometría curva (no euclidiana) no podemos encontrar un conjunto de coordenadas que sean mutuamente perpendiculares, donde las líneas de coordenadas son todas paralelas a cada cuadrícula tiene la misma área., Es posible que encontremos un sistema de coordenadas donde podamos hacer algunos de estos pero no todos.
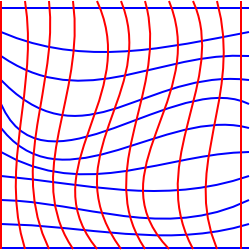
Este diagrama intenta ilustrar esta situación en 2 dimensiones, aunque es un poco engañoso, porque lo hemos dibujado en un plano para que pudiéramos haber dibujado coordenadas rectangulares.
para tratar de ilustrar una situación donde esto es imposible podríamos pensar en un plano bidimensional que se ha estirado a la tercera dimensión.,

en esta situación podemos elegir coordenadas que forman una cuadrícula rectangular cuando se proyecta sobre un plano horizontal, sin embargo, a una persona que vive en la superficie, algunos de los cuadrados de la cuadrícula parecerán tener un área más grande que otros y las líneas de la cuadrícula pueden no parecer paralelas. No hay un sistema de coordenadas bidimensionales que preserve líneas paralelas, ángulos y áreas al mismo tiempo.,
un ejemplo similar es tratar de mapear la superficie de la tierra, podemos usar líneas de latitud y longitud, pero las líneas de longitud se acercan más cerca de los polos.
en estos casos podríamos trabajar en términos de coordenadas tridimensionales y ese es un enfoque que tomaremos con algunos tipos de geometrías no euclidianas. A menudo es posible incrustar una geometría particular en una geometría dimensional más alta para hacerla más euclidiana.,
a veces es el caso que, cuando miramos una geometría a gran escala que no es euclidiana, pero si lo miramos en una escala cada vez más pequeña, entonces se aproxima a una geometría euclidiana. Para hacer esto necesitamos encontrar un sistema de coordenadas donde los ángulos se preserven en cada punto, es decir, las líneas de coordenadas horizontales y verticales siempre deben intersectarse a 90° aunque las líneas no sean rectas. Esto se conoce como geometría conforme. En este tipo de geometría podemos al menos definir un sistema de coordenadas local.,
relacionado con esto es si la geometría puede ser diferenciada e integrada, una condición para esto es que debe ser bien comportada y no tener ningún salto repentino, etc. Algunas geometrías y sistemas de coordenadas pueden comportarse bien en algunos lugares, pero tienen singularidades, etc.
para obtener información sobre cómo se mide la curvatura, consulte esta página.
notación matemática
¿cómo tratamos las geometrías donde no podemos usar todas las reglas que se aplican a la geometría euclidiana?,
Un enfoque es usar Notación tensora, esto proporciona convenciones y notación que nos ayudan a cambiar entre diferentes sistemas de coordenadas. Un sistema de coordenadas ortogonales, local a cualquier punto, se puede definir mediante el uso de vectores base que son tangentes a las líneas de coordenadas.,Manifold
ver esta página
relación entre las geometrías hiperbólicas y Minkowski
| Geometría Minkowski | geometría hiperbólica | |
| punto | evento en el espacio tiempo | partícula en movimiento uniforme |
| distancia entre dos puntos | intervalo espacio-temporal entre dos eventos | velocidad relativa entre dos de estas partículas |
terminología
Aquí nos fijamos en la terminología como geometrías, espacios, modelos, proyecciones y transformaciones., Es bastante difícil cuando empezamos a tratar con geometrías no euclidianas porque usamos terminología similar a la que estamos acostumbrados en el espacio euclidiano convencional, pero los términos pueden tener propiedades ligeramente diferentes.,pruebe
la Geometría Elíptica
Modelos
Ejemplos son:
- media Superior-modelo de avión
- Poincaré modelo de disco
- Proyectiva modelo
- Conformación de modelo
Proyecciones
la Proyección Estereográfica
Transforma
Invariante
Ejemplos son:
- Transformación de Möbius
- Transformación de Lorentz
Postulado Paralelo
Si le quitas el postulado paralelo desde el Espacio Euclidiano.,
esto conduce a:
- El postulado paralelo es falso
- Los ángulos de un triángulo no agregan a π
- Para una forma de un tamaño dado, no existe en general una forma similar de un tamaño más grande.,activa
conformal (Poincaré disco ) las líneas rectas – geodesics segmentos de círculos el ángulo conservar más los ángulos internos del triángulo π-(α+β+γ)=CΔ la distancia entre dos puntos con