resolver ecuaciones numéricamente

encontrar todas las raíces de una función polinómica

Use vpasolve para encontrar todas las soluciones a la función f(x)=6X7-2×6+3×3-8.

syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)

syms xh = fplot(exp(x/7)*cos(2*x),);grid on

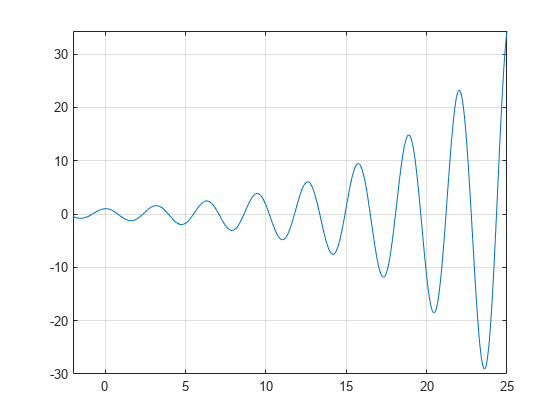
el Uso de vpasolve para encontrar un cero de la función f. Tenga en cuenta que vpasolve devuelve solo una solución de una ecuación no polinomial, incluso si existen múltiples soluciones., On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3 vpasolve(f,x,'Random',true)end

ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')

ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')

ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')

To find a zero close to x=10, set the starting point to 10.,

vpasolve(f,x,10)

ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')

Para encontrar el cero cerca de x=1000, establecer el punto de partida para 1000.

vpasolve(f,x,1000)

ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')

Para encontrar el cero en el rango de 15≤x≤25, establecer el rango de búsqueda para .,

vpasolve(f,x,)

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

encontrar varios ceros en el intervalo , usted no puede llamar a vpasolve repetidas veces, porque devuelve el mismo resultado en cada llamada, como se ha demostrado. En su lugar, establezca el rango de búsqueda y establezca 'Random' en true.,

for k = 1:3 vpasolve(f,x,,'Random',true)end

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')

Porque 'Random' selecciona puntos de partida al azar, la misma solución podría encontrarse en las sucesivas llamadas.,

buscar todos los ceros en un rango de búsqueda especificado

crear una función findzerospara encontrar sistemáticamente todos los ceros para f en un rango de búsqueda dado, dentro de una tolerancia de error especificada. La función comienza con el rango de búsqueda de entrada y llama a vpasolve para encontrar un cero. Luego, divide el rango de búsqueda en dos alrededor del valor cero y recursivamente se llama a sí mismo con los nuevos rangos de búsqueda como entradas para encontrar más ceros.

La función se explica sección por sección aquí.,

Declare la función con las tres entradas y una salida. La primera entrada es la función, la segunda entrada es el rango, y la tercera entrada opcional le permite especificar el error entre un cero y los límites superior e inferior generados a partir de él.

function sol = findzeros(f,range,err)

Si no se especifica el argumento opcional para el error, la tolerancia, el findzeros marca err a 0.001.

if nargin < 2 err = 1e-3;end

Encontrar un cero en el intervalo de búsqueda utilizando vpasolve.,

sol = vpasolve(f,range);

Si vpasolve no encontrar un cero, la salida.

if(isempty(sol)) return

Si vpasolve encuentra un cero, dividir el rango de búsqueda en dos rangos de búsqueda por encima y por debajo del cero.

else lowLimit = sol-err; highLimit = sol+err;

Llamada findzeros con la parte inferior del rango de búsqueda. Si findzeros devuelve ceros, copie los valores en la matriz de soluciones y ordénelos.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end

Llamada findzeros con el mayor rango de búsqueda., Si findzeros devuelve ceros, copie los valores en la matriz de soluciones y ordénelos.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend

toda La función findzeros es como sigue. Guarde esta función como findzeros.m en la carpeta actual.

syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'

Obtener Soluciones de Precisión Arbitraria

el Uso de digits para establecer la precisión de las soluciones que devuelve vpasolve., Por defecto, vpasolve devuelve soluciones con una precisión de 32 cifras significativas.

f = exp(x/7)*cos(2*x);vpasolve(f)

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

el Uso de digits para aumentar la precisión de 64 cifras significativas. Al modificar digits, asegúrese de guardar su valor actual para poder restaurarlo.,

digitsOld = digits;digits(64)vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')

a continuación, cambiar la precisión de las soluciones a 16 cifras significativas.

digits(16)

Resolver Multivariante de Ecuaciones Utilizando Rangos de Búsqueda

Considere el siguiente sistema de ecuaciones.

Una parcela de las ecuaciones para 0≤x≤2.5 y 0≤x≤2.5 muestra que las tres superficies se cortan en dos puntos., Para visualizar mejor la gráfica, utilice view. Para escalar los valores del mapa de colores, use caxis.

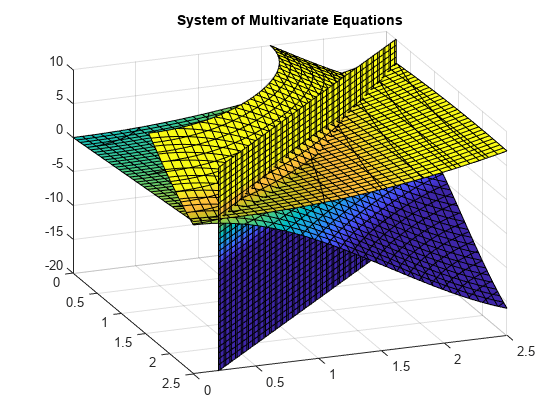
el Uso de vpasolve para encontrar un punto donde las superficies se cruzan. La función vpasolve devuelve una estructura. Para acceder a la etiqueta x, y y z-los valores de la solución, el índice de la estructura.,

sol = vpasolve(equations);

búsqueda de una región en el espacio de la solución, especificar la búsqueda rangos de las variables. Si especifica los rangos 0≤x≤1.5 y 1.5≤y≤2.5, entonces vpasolve la función busca en el área delimitada que se muestra.

el Uso de vpasolve para encontrar una solución para este rango de búsqueda. Para omitir un rango de búsqueda para z, establezca el Tercer Rango de búsqueda en .,

vars = ;range = ;sol = vpasolve(equations, vars, range);

Para encontrar múltiples soluciones, establecer el 'Random' opción true. Esto hace que vpasolve use puntos de inicio aleatorios en ejecuciones sucesivas. La opción 'Random' se puede usar junto con rangos de búsqueda para hacer que vpasolve use puntos de partida aleatorios dentro de un rango de búsqueda. Debido a que 'Random' Selecciona los puntos de inicio al azar, la misma solución podría encontrarse en llamadas sucesivas., Llame a vpasolve repetidamente para asegurarse de encontrar ambas soluciones.

trazar las ecuaciones. Superponer las soluciones como un gráfico de dispersión de puntos con amarillo X marcadores usando scatter3. Para visualizar mejor la gráfica, haga que dos de las superficies sean transparentes usando alpha. Escala el mapa de colores a los valores de la gráfica usando caxis, y cambia la perspectiva usando view.

vpasolve encuentra soluciones en la intersección de las superficies formadas por las ecuaciones como se muestra.,

Lastly, restore the old value of digits for further calculations.

digits(digitsOld)