propiedades de áreas
centroide
el centroide de una forma representa el punto sobre el cual el área de la sección se distribuye uniformemente. Si el área es doblemente simétrica alrededor de dos ejes ortogonales, el centroide se encuentra en la intersección de esos ejes. Si el área es simétrica alrededor de un solo eje, entonces el centroide se encuentra en algún lugar a lo largo de ese eje (la otra coordenada tendrá que ser calculada)., Si la ubicación exacta del centro de gravedad no se puede determinar por la inspección, se puede calcular por:
|
|
|
donde dA representa el área de un infinitesimalmente pequeño elemento, a es el área total de la sección transversal, y x y y son las coordenadas del elemento dA con respecto al eje de interés.,
las ubicaciones centroidales de las secciones transversales comunes están bien documentadas, por lo que normalmente no es necesario calcular la ubicación con las ecuaciones anteriores., de formas básicas cuyo centroide lugares son conocidos con respecto a algún punto de referencia, entonces el centroide de la ubicación de los compuestos de sección transversal puede ser calculado como:
|
|
|
donde xc y yc,i son las coordenadas rectangulares de la ubicación del centroide de la i-ésima de la sección con respecto al punto de referencia, y Ai es el área de la i-ésima sección.,
distancia Centroidal
la distancia centroidal, c, es la distancia desde el centroide de una sección transversal a la fibra extrema., La distancia centroidal en la dirección y para una sección transversal rectangular se muestra en la siguiente figura:
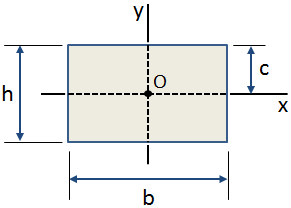
los usos comunes para la distancia centroidal incluyen:
- calcular el esfuerzo de flexión máximo en una sección transversal
- calcular el valor del primer momento de área, Q, arriba un punto en la sección transversal para determinar el esfuerzo cortante en ese punto
tenemos una serie de calculadoras estructurales para elegir.,
- Calculadora de vigas
- unión Atornillada de la Calculadora
- Perno Patrón de Distribución de la Fuerza
- Lug Calculadora
- Columna de Pandeo de la Calculadora
- la Fatiga Crecimiento de las grietas de la Calculadora

Primer Momento de Área
El primer momento de un área con respecto a un eje de interés se calcula como:
| Qx = ∫ y dA | Qy = ∫ x dA |
donde Qx es el primer momento sobre el eje x y Qy es el primer momento sobre el eje.,Si el área está compuesta de una colección de formas básicas cuyo centroide lugares son conocidos con respecto al eje de interés, entonces el primer momento de la composición área puede ser calculada como:
|
|
|
tenga en cuenta que el primer momento del área se utiliza a la hora de calcular el centroide de la sección transversal con respecto a algunas de origen (como se discutió anteriormente)., El primer momento también se utiliza para calcular el valor de la tensión de corte en un punto particular de la sección transversal. En este caso, el primer momento se calcula para un área que constituye una porción más pequeña de la sección transversal, donde el área está limitada por el punto de interés y la fibra extrema (superior o inferior) de la sección transversal. El primer momento se calcula sobre un eje que pasa a través del centroide de la sección transversal.,
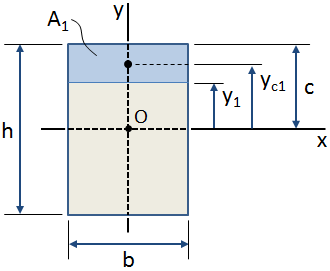
en la figura anterior, el área azul sombreada es el área de interés dentro de la sección transversal general.,nt de esta área con respecto al eje x (que pasa a través del centroide de sección transversal, punto O en la figura anterior) se calcula como:
Si se conoce la ubicación centroidal del área de interés, entonces el primer momento el área con respecto al eje se puede calcular como (consulte la figura anterior):
cabe señalar que el primer momento de un área será positivo o negativo dependiendo de la posición de la posición del área con respecto al eje de interés., Por lo tanto, el primer momento de toda el área de una sección transversal con respecto a su propio centroide será cero.
momento de inercia del área
el segundo momento de área, más comúnmente conocido como el momento de inercia, I, de una sección transversal es una indicación de la capacidad de un miembro estructural para resistir la flexión.,(Nota 1) Ix e Iy son los momentos de inercia sobre los ejes x E y, respectivamente, y se calculan mediante:
| Ix = ∫ Y2 dA | Iy = ∫ x2 dA |
donde x E y son las coordenadas del elemento dA con respecto al eje de interés.
más comúnmente, los momentos de inercia se calculan con respecto al centroide de la sección. En este caso se les conoce como momentos de inercia centroidales y se denotan como Icx para la inercia sobre el eje x y Icy para la inercia sobre el eje Y.,
los momentos de inercia de las secciones transversales comunes están bien documentados, por lo que normalmente no es necesario calcularlos con las ecuaciones anteriores. Las propiedades de varias secciones transversales comunes se dan al final de esta página.
si una sección transversal se compone de una colección de formas básicas cuyos centroides son todos coincidentes, entonces el momento de inercia de la sección compuesta es simplemente la suma de los momentos individuales de inercia. Un ejemplo de esto es una viga de caja que consta de dos secciones rectangulares, como se muestra a continuación., En este caso, la sección exterior tiene » área positiva «y la sección interior tiene» área negativa», por lo que el momento compuesto de inercia es la sustracción del momento de inercia de la sección interior de la sección exterior.
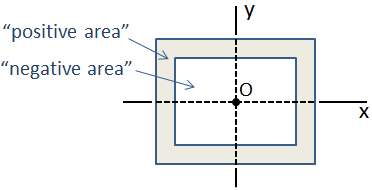
en el caso de una sección transversal compuesta más complicada en la que las ubicaciones centroidales no son coincidentes, el momento de inercia se puede calcular utilizando el teorema del eje paralelo.
es importante no confundir el momento de inercia de un área con el momento de inercia de un cuerpo sólido., El momento de inercia del área indica la resistencia de una sección transversal a la flexión, mientras que el momento de inercia de la masa indica la resistencia de un cuerpo a la rotación.,
teorema del eje paralelo
Si se conoce el momento de inercia de una sección transversal sobre un eje centroidal, entonces el teorema del eje paralelo se puede usar para calcular el momento de inercia sobre cualquier eje paralelo:
donde Ic es el momento de inercia sobre el eje centroidal, d es la distancia entre el eje centroidal y el eje paralelo, y a es el área de la sección transversal.,
si una sección transversal se compone de una colección de formas básicas cuyos momentos de inercia centroidales se conocen junto con las distancias de los centroides a algún punto de referencia, entonces el teorema del eje paralelo se puede utilizar para calcular el momento de inercia de la sección transversal compuesta.
por ejemplo, un I-Beam puede ser aproximado por 3 rectángulos, como se muestra a continuación. Dado que esta sección compuesta es simétrica sobre los ejes x E y, el centroide de la sección se puede ubicar mediante inspección en la intersección de esos ejes. El centroide se encuentra en el origen, O, en la figura.,
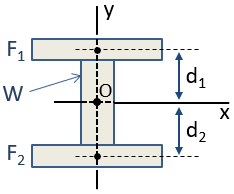
el momento de inercia de la sección compuesta se puede calcular utilizando el teorema del eje paralelo. El momento de inercia centroidal de la sección Sobre el eje x, Icx, se calcula como:
donde los Términos Icx son los momentos de inercia de las secciones individuales sobre sus propios centroides en la orientación del eje x, los Términos d son las distancias de los centroides de sección individuales al centroide de sección compuesta, y los Términos A son las áreas de las secciones individuales. Debido a que el centroide de la sección W y el centroide de la sección compuesta son coincidentes, d es cero para esa sección y por lo tanto no hay término Ad2.,
es importante tener en cuenta la implicación del teorema del eje paralelo que a medida que una sección individual se mueve más lejos del centroide de la sección compuesta, la contribución de esa sección al momento de inercia de la sección compuesta aumenta en un factor de d2. Por lo tanto, si la intención es aumentar el momento de inercia de una sección sobre un eje en particular, es más eficiente ubicar el área lo más lejos posible de ese eje. Esto explica la forma de una viga en I., Las bridas son los principales contribuyentes al momento de inercia, y la banda sirve para separar las bridas del eje de flexión. La tela no necesita mantener un poco de espesor sin embargo para evitar pandeo y porque la tela toma una parte significativa de la tensión de corte en la sección.
momento Polar de inercia
el momento polar de inercia, I, de una sección transversal es una indicación de la capacidad de un miembro estructural para resistir la torsión alrededor de un eje perpendicular a la sección., El momento polar de inercia para una sección con respecto a un eje se puede calcular por:
donde x E y son las coordenadas del elemento dA con respecto al eje de interés, y r es la distancia entre el elemento dA y el eje de interés.,
aunque el momento polar de inercia se puede calcular utilizando la ecuación anterior, Normalmente es más conveniente calcularlo utilizando el teorema del eje perpendicular, que establece que el momento polar de inercia de un área es la suma de los momentos de inercia alrededor de dos ejes ortogonales que pasan a través del eje de interés:
más comúnmente, el eje de interés pasa a través centroide de la sección transversal.,
Módulo de sección
la tensión de flexión máxima en una viga se calcula como σb = Mc / Ic, donde c es la distancia desde el eje neutro hasta la fibra extrema, IC es el momento centroidal de inercia, y M es el momento de flexión. El módulo de sección combina los Términos C e Ic en la ecuación de esfuerzo de flexión:
Usando el módulo de sección, el esfuerzo de flexión se calcula como σb = M / S. La utilidad del módulo de sección es que caracteriza la resistencia a la flexión de una sección transversal en un solo término., Esto permite la optimización de la sección transversal de una viga para resistir la flexión al maximizar un solo parámetro.
radio de Giro
El radio de giro representa la distancia desde el centroide de una sección en la que toda el área podría concentrarse sin tener ningún efecto en el momento de inercia.,>
A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:
The rectangular radii of gyration can also be used to calculate the polar radius of gyration:
We have a number of structural calculators to choose from., Estos son solo algunos:
- Calculadora de haz
- Calculadora de unión atornillada
- Distribución de fuerza de patrón de Perno
- Calculadora de estirón
- Calculadora de pandeo de columna
- Calculadora de crecimiento de grietas por fatiga

propiedades de las secciones transversales comunes
la siguiente tabla muestra las propiedades de las secciones transversales comunes. Se pueden encontrar tablas más extensas en las referencias listadas.
Las propiedades calculadas en la tabla incluyen área, momento de inercia centroidal, módulo de sección y radio de giro.,
Tenemos un número de estructural calculadoras para elegir., Estos son solo algunos:
- Calculadora de haz
- Calculadora de unión atornillada
- Distribución de fuerza de patrón de Perno
- Calculadora de estirón
- Calculadora de pandeo de columna
- Calculadora de crecimiento de grietas por fatiga

notas
Nota 1: deflexión de una viga
la deflexión de una viga en flexión está determinada por el momento de inercia de la sección transversal, la longitud de la viga y el módulo elástico del material. Más detalles se dan en esta discusión de la desviación del haz.