Logarithmische Funktionen sind die Inversen Exponentialfunktionen. Die Umkehrung der Exponentialfunktion y = ax ist x = ay. Die logarithmische Funktion y = logax ist als Äquivalent zur Exponentialgleichung x = ay definiert. y = logax nur unter den folgenden Bedingungen: x = ay, a > 0 und a≠1. Es wird die logarithmische Funktion mit der Basis a genannt.
Überlegen Sie, was die Umkehrung der Exponentialfunktion bedeutet: x = ay., Bei einer Zahl x und einer Basis a, zu welcher Potenz y muss a auf gleich x erhöht werden? Dieser unbekannte Exponent y entspricht logax. Sie sehen also, dass ein Logarithmus nichts anderes als ein Exponent ist. Per Definition ist alogax = x für jedes echte x > 0.
Unten sind Graphen der Form y = logax abgebildet, wenn a > 1 und wenn 0 < a < 1. Beachten Sie, dass die Domäne nur aus den positiven reellen Zahlen besteht und dass die Funktion immer zunimmt, wenn x zunimmt.,
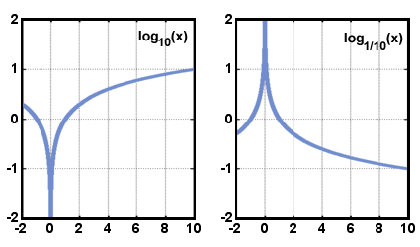
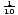 x.
x.Die Domäne einer logarithmischen Funktion sind reelle Zahlen größer als Null und der Bereich sind reelle Zahlen. Der Graph von y = logax ist symmetrisch zum Graph von y = ax in Bezug auf die Linie y = x. Diese Beziehung gilt für jede Funktion und ihre Inverse. ,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(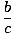 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
Eine Natürliche logarithmische Funktion ist eine Logarithmusfunktion mit der Basis e. f (x) = logex = ln x, wobei x > 0. ln x ist nur eine neue Form der Notation für Logarithmen mit Basis e. Die meisten Rechner haben Schaltflächen mit der Bezeichnung „log“ und „ln“. Die Schaltfläche“ log „geht davon aus, dass die Basis zehn ist, und die Schaltfläche“ ln “ lässt die Basis natürlich gleich e., Die logarithmische Funktion mit Basis 10 wird manchmal als gemeinsame logarithmische Funktion bezeichnet. Es ist weit verbreitet, weil unsere nummerierung system hat basis zehn. Natürliche Logarithmen werden häufiger im Kalkül gesehen.
Es existieren zwei Formeln, mit denen die Basis einer logarithmischen Funktion geändert werden kann. Der erste gibt Folgendes an: logab = 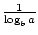 . Die bekanntere und nützlichere Formel zum Ändern von Basen wird allgemein als Änderung der Basisformel bezeichnet. Es erlaubt, die Basis einer logarithmischen Funktion in eine beliebige positive reelle Zahl ≠1 zu ändern. Es besagt, dass logax =
. Die bekanntere und nützlichere Formel zum Ändern von Basen wird allgemein als Änderung der Basisformel bezeichnet. Es erlaubt, die Basis einer logarithmischen Funktion in eine beliebige positive reelle Zahl ≠1 zu ändern. Es besagt, dass logax = 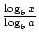 ., In diesem Fall sind a, b und x alle positiven reellen Zahlen und a, b≠1.
., In diesem Fall sind a, b und x alle positiven reellen Zahlen und a, b≠1.
Im nächsten Abschnitt werden wir einige Anwendungen von exponentiellen und logarithmischen Funktionen diskutieren.