Le « Cercle Unité » est un cercle de rayon 1.
Étant simple, il est un excellent moyen d’apprendre et de parler des longueurs et des angles.
Le Centre est placé sur un graphique où l’axe x et l’axe y se croisent, nous obtenons donc cet arrangement soigné ici.
le Sinus, le Cosinus et la Tangente
Car le rayon est de 1, on peut mesurer directement les sinus, cosinus et tangente.,
Ce qui se passe lorsque l’angle θ, est de 0°?
cos de 0° = 1, sin 0° = 0 et tan 0° = 0
Ce qui se passe lorsque θ est de 90°?
cos 90° = 0, sin 90° = 1 et tan 90° n’est pas défini
l’Essayer Vous-même!
essayer!, Déplacez la souris pour voir comment différents angles (en radians ou en degrés) affectent le sinus, le cosinus et la tangente
les « côtés » peuvent être positifs ou négatifs selon les règles des coordonnées cartésiennes. Cela fait également changer le sinus, le cosinus et la tangente entre les valeurs positives et négatives.
essayez également le cercle de L’unité Interactive.,
Pythagore
Le théorème de Pythagore dit que pour un triangle rectangle, le carré du côté long est égal à la somme des carrés du côté long deux autres côtés:
X2 + Y2 = 12
Mais 12 est juste 1, donc:
X2 + Y2 = 1
(l’équation du cercle unité)
aussi, puisque x=cos et y=sin, nous obtenons:
(COS(θ))2 + (sin(θ))2 = 1
Une « identité »utile
angles importants: 30°, 45° et 60°
Vous devriez essayer de vous rappeler sin, cos et Tan pour les angles 30°, 45° et 60°.,
Oui, Oui, c’est une douleur de devoir se souvenir des choses, mais cela vous facilitera la vie quand vous les connaissez, pas seulement aux examens, mais à d’autres moments où vous devez faire des estimations rapides, etc.
Ce sont les valeurs dont vous devriez vous souvenir!,id= »0f47f3223b »>
What about tan?,
Eh bien, tan = sin / cos, donc nous pouvons le calculer comme ceci:
tan (30°) =sin (30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan (45°) =sin (45°)cos(45°) = √2/2√2/2 = 1
tan (60°) =sin (60°)cos(60°) = √3/21/2 = √3
* Remarque: écrire 1√3 peut vous coûter des marques (voir dénominateurs rationnels), alors utilisez plutôt √33
croquis rapide
Une autre façon de vous aider à vous souvenir de 30° et 60° est de faire un croquis rapide:
| dessinez un triangle avec des longueurs de ID= »466963d716″> |
|
couper en deux.,div id= »56c966b492″> exemple: sin(30°)sinus: sactahtoa sinus est opposé divisé par hypoténuse
sin(30°) = oppositehypotenuse = 12
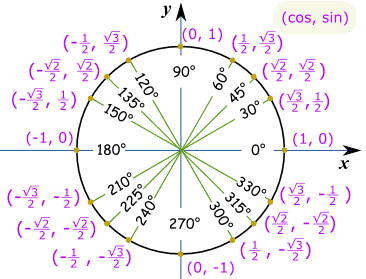
le cercle entierpour le cercle entier, nous avons besoin de valeurs dans chaque quadrant, avec le signe plus ou moins correct selon les coordonnées cartésiennes: notez que Cos est premier et SIN est deuxième, donc ça va (cos, sin):
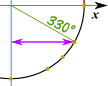
enregistrer au format pdf exemple: qu’est-ce que cos(330°) ?,
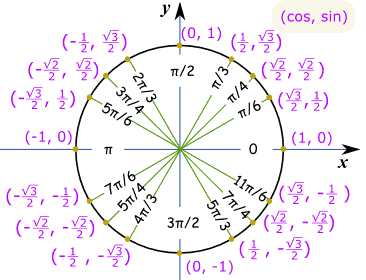
Faire un croquis de ce genre, et nous pouvons voir que c’est la version « longue » de la valeur: √32 Et c’est le même Cercle Unité en radians.
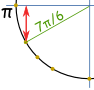
Exemple: qu’est-Ce que le péché(7π/6) ?
Pense que « 7π/6 = π + π/6 », puis faites un croquis. On peut alors voir qu’il est négatif et le « court » de la valeur: −½ |