Contenu – une accélération Constante

Contenu

une accélération Constante

Nous sommes tous familiers avec le fait qu’une voiture accélère lorsque nous avons mis le pied sur l’accélérateur. Le taux de changement de la vitesse d’une particule par rapport au temps est appelé son accélération. Si la vitesse de la particule change à une vitesse constante, alors ce taux est appelé l’accélération constante.,

par exemple, si la vitesse d’une particule se déplaçant en ligne droite change uniformément (à un taux de changement constant) de 2 m/s à 5 m/s sur une seconde, alors son accélération constante est de 3 m/s\(^2\).

vitesse décroissante

Si une particule a une vitesse initiale de 6 m/s et une accélération constante de \(-2\) m/s\(^2\), alors:

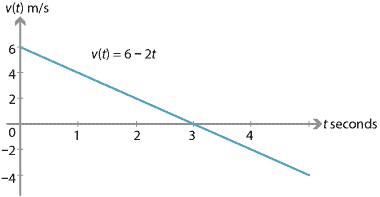
Au cours des trois premières secondes, la vitesse de la particule diminue (la particule ralentit). Après trois secondes, la particule est momentanément au repos., Après trois secondes, la vitesse diminue toujours, mais la vitesse augmente (la particule va de plus en plus vite).

Résumé

Si nous supposons que le taux de variation de la vitesse (accélération) est une constante, alors la constante d’accélération est donnée par

\

Plus précisément, l’accélération constante \(a\) est donnée par la formule suivante:

\

où \(v(t_i)\) est la vitesse à l’instant \(t_i\). Puisque la vitesse est un vecteur, est l’accélération.,

les formules d’accélération constante pour le mouvement en ligne droite

tout au long de cette section, nous avons examiné le mouvement en ligne droite avec une accélération constante. Cette situation est très courante; par exemple, un corps se déplaçant sous l’influence de la gravité se déplace avec une accélération constante.

Il est supposé que le mouvement commence lorsque \(t = 0\), et que la position initiale est prise comme origine, qui est, \(x(0) = 0\).,

Les cinq équations de mouvement

1. \(v = u + a\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}at^2\)
4. \(v^2 = u^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}at^2\)

Remarque. Chacun des cinq équations impliquent quatre des cinq variables \(u, v, x, a, t\). Si les valeurs de trois des variables sont connues, les valeurs restantes peuvent être trouvées en utilisant deux des équations.,

dérivant les formules d’accélération constante

la première équation du mouvement

puisque l’accélération est constante, on a \(a = \dfrac{v-u}{t}\). Cela donne la première équation du mouvement, \(v = u + at\).

La deuxième équation du mouvement

La deuxième équation,

\

dit que le déplacement est obtenu en multipliant la moyenne de la période initiale et finale de vitesses par le temps écoulé pendant le mouvement. Plus simplement:

\

Nous pouvons dériver cette équation en utilisant le fait que le déplacement est égal à la zone signée sous le graphique vitesse–temps.,

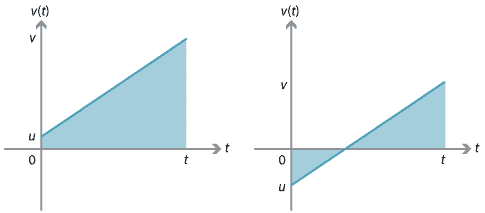
Pour le graphique sur la droite, le déplacement peut être trouvé en considérant les deux triangles entre le graphique et le \(t\) de l’axe. L’un des triangles est positif signé et l’autre est négative signé zone.

trouver le déplacement d’une particule à partir du graphique vitesse–temps en utilisant l’intégration sera discuté dans une section ultérieure de ce module.,

La troisième équation du mouvement

en Remplaçant par \(v\) à partir de la première équation dans la seconde équation donne

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+a)t}{2} \\ &= \dfrac{2ut+a^2}{2} \\ &= ut + \dfrac{1}{2}at^2, \end{align*}

qui est la troisième équation. Ainsi \(x\) est un quadratique dans \(t\), et donc le graphe de \(x\) contre \(t\) est une parabole.

la quatrième équation du mouvement

de la première équation, Nous avons \(t = \dfrac{v-u}{a}\)., En substituant dans la deuxième équation donne

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{align*}

Réorganiser pour faire \(v^2\) le produit de la quatrième équation: \(v^2 = u^2 + 2ax\).

La cinquième équation du mouvement

à Partir de la première équation, nous avons \(u = v-at\)., À l’aide de la deuxième équation, on obtient

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v a+v)t}{2} \\ &= \dfrac{2vt-à^2}{2} \\ &= vt-\dfrac{1}{2}at^2, \end{align*}

qui est la cinquième équation.

mouvement Vertical

Le mouvement dû à la gravité est un bon contexte pour démontrer l’utilisation des formules d’accélération constante., Comme nous l’avons vu précédemment, nos deux directions en mouvement vertical sont de haut en bas, et une décision doit être prise quant à laquelle des deux directions est positive. L’accélération due à la gravité est une constante, avec une amplitude notée \(g\). Dans l’exemple suivant, nous prenons la direction vers le haut pour être positif et prenons \(g = 10\) m/s\(^2\).

Plus d’utiliser les équations de mouvement

Next page – Content – Average velocity and average speed