
La fonction delta de Dirac est une fonction introduite en 1930 par le P. A. M. Dirac dans son livre majeur sur la mécanique quantique. Un modèle physique qui visualise une fonction delta est une distribution de masse de masse totale finie M – l’intégrale sur la distribution de masse., Lorsque la distribution devient de plus en plus petite, alors que M est constant, la distribution de masse se réduit à une masse ponctuelle, qui par définition a une étendue nulle et a pourtant une intégrale de valeur finie égale à la masse totale M. à la limite d’une masse ponctuelle, la distribution devient une fonction delta de Dirac.
Heuristiquement, la fonction delta de Dirac peut être vue comme une extension du delta de Kronecker des indices intégraux (éléments de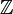 ) aux indices réels (éléments de
) aux indices réels (éléments de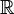 )., Notez que le delta de Kronecker agit comme un « filtre » dans une sommation:
)., Notez que le delta de Kronecker agit comme un « filtre » dans une sommation:
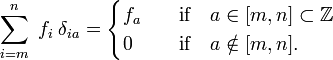
par analogie, la fonction delta de Dirac δ(x−a) est définie par (remplacer i par x et la sommation sur i par une intégration sur x),
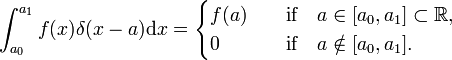
la fonction delta de Dirac div id= »D4efe881a0″>, mais une distribution, également connue sous le nom de fonction incorrecte ou généralisée. Les physiciens expriment son caractère spécial en déclarant que la fonction delta de Dirac n’a de sens que comme facteur dans une intégrande (« sous l’intégrale »)., Les mathématiciens disent que la fonction delta est une fonction linéaire sur un espace de fonctions de test.
table des Matières
- 1 Propriétés
- 2 Delta-convergente séquences
- 2.1 Bloc de fonctions
- 2.2 Gaussien fonctions
- 2.3 Lorentz-de Cauchy de fonctions
- 2.4 Sinc fonctions
- 3 produits Dérivés de la fonction delta
- 3.,1 Propriétés de la dérivée
- 4 Primitive
- 5 La fonction delta de Dirac en trois dimensions
- 6 Références
Propriétés
Plus généralement on prend la basse et la limite supérieure de la définition de la fonction delta égal à 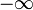 et
et 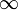 , respectivement. À partir de là, ce sera fait.
, respectivement. À partir de là, ce sera fait.
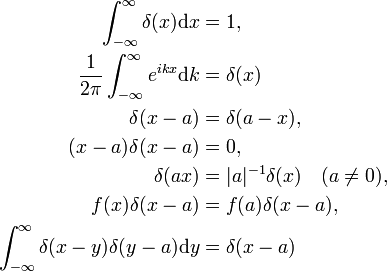
la preuve de ces propriétés par le physicien procède en effectuant des substitutions appropriées dans l’intégrale et en utilisant les règles ordinaires du calcul intégral., La fonction delta en tant que transformée de Fourier de la fonction unitaire f(x) = 1 (la deuxième propriété) sera prouvée ci-dessous. La dernière propriété est l’analogie de la multiplication de deux identité des matrices,
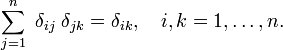
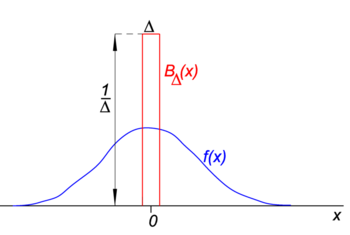
Fig. 1. Fonction Block (« boxcar ») (rouge) fois la fonction régulière f (x) (Bleu).
séquences Delta-convergentes
Il existe des familles de fonctions régulières Fa(x) dont les membres de la famille diffèrent par la valeur d’un seul paramètre α., Un exemple d’une telle famille est formée par la famille de fonctions gaussiennes Fa(x) = exp(−ax2), où les différentes valeurs du paramètre unique α distinguent les différents membres. Lorsque tous les membres sont linéairement normalisables, c’est-à-dire que l’intégrale suivante est finie indépendamment de α,
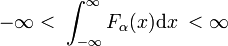
et que tous les membres culminent autour de x = 0, alors la famille peut former une séquence delta-convergente.,
Fonctions de bloc
l’exemple le plus simple d’une séquence Delta-convergente est formé par la famille de fonctions de bloc, caractérisée par Δ positif,
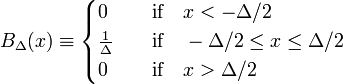
sur la Fig. 1 la fonction de bloc BΔ est affichée en rouge. Évidemment, l’aire (largeur fois hauteur) sous la courbe rouge est égale à l’unité, quelle que soit la valeur de Δ,
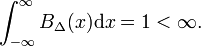
soit la fonction arbitraire f(x) (bleu sur la Fig. 1) être continu (Pas de sauts) et fini au voisinage de x=0., Lorsque Δ devient très petit, et la fonction de bloc très étroite (et nécessairement très élevée car largeur fois hauteur est constante) le produit f(x) BΔ(x) devient en bonne approximation égal à f(0) BΔ(x). Plus le bloc est étroit, meilleure est l’approximation., Par conséquent, pour Δ allant à zéro,
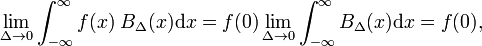
qui peut être comparée à la définition de la fonction delta,
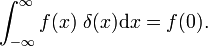
cela montre que la famille de fonctions de bloc converge vers la fonction delta de Dirac pour le paramètre Δ décroissant; la famille forme une séquence delta-convergente:
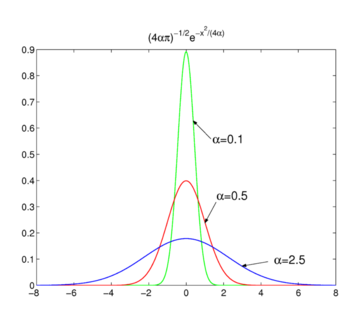
Fig. 2. Fonctions gaussiennes.
Remarque: Nous avons intégré sur l’ensemble de l’axe réel., Évidemment ce n’est pas nécessaire, on aurait pu exclure les ailes à valeur nulle de la fonction bloc et ne les intégrer que sur la bosse au milieu, de-Δ/2 à +Δ/2. Dans les textes mathématiques, comme par exemple Ref. , ce raffinement dans les limites d’intégration est inclus dans la définition de la séquence delta-convergente. C’est, il est nécessaire que les intégrales sur les deux ailes disparaissent dans la limite de. Étant donné que les séquences Delta-convergentes rencontrées dans les applications physiques satisfont généralement à cette condition, nous omettons la définition mathématique la plus exacte.,
Gaussien fonctions
Considérer la famille,
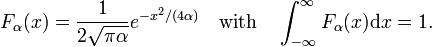
Comme indiqué dans la Fig. 2 les fonctions culminent autour de x = 0 et deviennent plus étroites pour diminuer α. Pourquoi la famille de fonctions Gaussiennes forme un delta-convergente séquence,
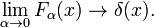
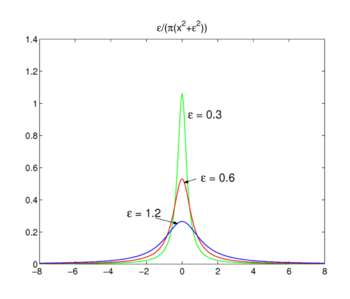
Fig. 3. Fonctions de Lorentz-Cauchy
Fonctions de Lorentz-Cauchy
la famille de fonctions représentée à la Fig., 3
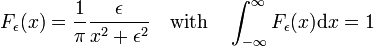
forms a delta-convergent sequence,
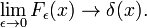
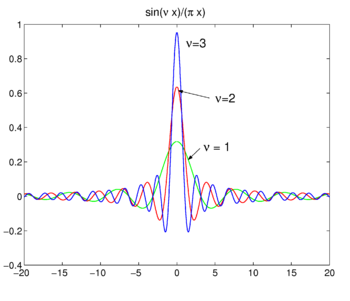
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 est
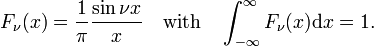
Cette famille converge vers la fonction delta de l’augmentation de ν
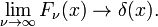
Cette limite conduit facilement à la représentation intégrale de Fourier de la fonction delta:
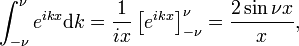
alors que
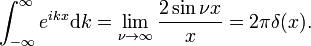
La fonction delta de Dirac est la transformée de Fourier de l’unité de la fonction f(x) = 1.
dérivées de la fonction delta
considérons une fonction différentiable f(x) qui disparaît à plus et moins l’infini.,d= »ed7dae11d6″>
de la même manière que l’on prouve la règle de turnover et L’Hermiticité de l’opérateur de momentum mécanique quantique 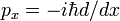 , nous avons montré ici que d/dx est anti-hermitien,
, nous avons montré ici que d/dx est anti-hermitien,
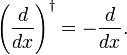
En effet, lorsque l’on écrit intégration et disparition de F(X) sur les limites d’intégration que
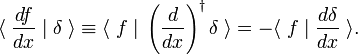
cette règle de turnover est utilisée comme définition de la dérivée de la fonction delta,
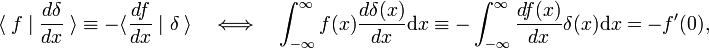
où le premier indique la dérivée première de f(x)., Selon la définition de la fonction delta, la dérivée première est évaluée en x = 0. En utilisant m fois la règle de turnover, il s’ensuit que la dérivée mth de la fonction delta est définie par
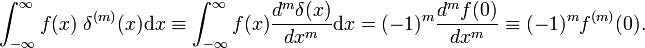
propriétés de la dérivée
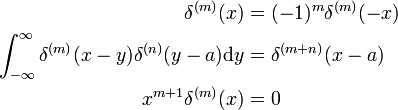
ces résultats peuvent être prouvés en faisant la substitution x → −x et en utilisant la règle de turnover pour d/dx (voir ci-dessus).,
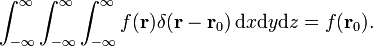
Les trois dimensions de la fonction delta peut être factorisée
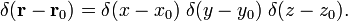
Dans sphérique coordonnées polaires
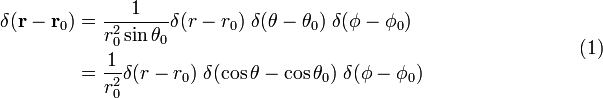
la Preuve de l’équation (1)
Écrire
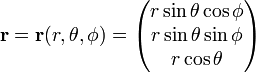
Le Jacobien (Jacobi, déterminant) de cette transformation de coordonnées Cartésiennes, sphériques coordonnées polaires est
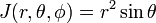
de Considérer
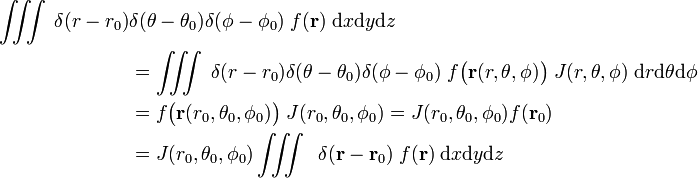
alors que
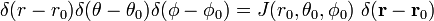
et
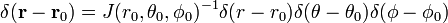
La dernière ligne de l’équation (1) suit à partir de la chaîne de la règle.,
voici utiles et fréquemment appliqué propriété est prouvé ici,
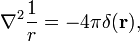
où ∇2 est le Laplacien dans les trois dimensions de coordonnées Cartésiennes et r est la longueur de la r.