les fonctions Logarithmiques sont les inverses des fonctions exponentielles. L’inverse de la fonction exponentielle y = ax x = ay. La fonction logarithmique y = logax est équivalente à l’équation exponentielle x = ay. y = logax uniquement dans les conditions suivantes: x = ay, un > 0 et a≠1. On l’appelle la fonction logarithmique de base a.
considérez ce que signifie l’inverse de la fonction exponentielle: x = ay., Étant donné un nombre x et une base a, à quelle puissance y a doit-il être élevé à x égal? Cet exposant Inconnu, y, est égal à logax. Vous voyez donc qu’un logarithme n’est rien de plus qu’un exposant. Par définition, alogax = x, pour chaque x réel > 0.
ci-Dessous sont représentés les graphiques de la forme y = logax lorsqu’un > 1 0 < < 1. Notez que le domaine se compose uniquement des nombres réels positifs, et que la fonction augmente toujours à mesure que x augmente.,
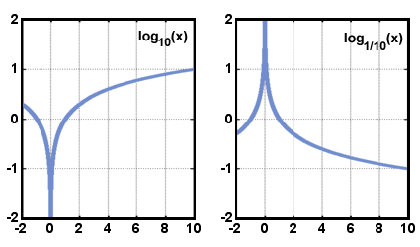
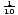 X.
X.le domaine d’une fonction logarithmique est des nombres réels supérieurs à zéro, et la plage est des nombres réels. Le graphe de y = logax est symétrique au graphe de y = ax par rapport à la droite y = X. Cette relation est vraie pour toute fonction et son inverse. ,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(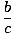 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
naturelle d’Une fonction logarithme est une fonction logarithmique de base e. f (x) = logex = ln x, où x > 0. ln x est juste une nouvelle forme de notation pour les logarithmes avec la base E. La plupart des calculatrices ont des boutons étiquetés « log » et « ln ». Le bouton » log « suppose que la base est dix, et le bouton » ln », bien sûr, laisse la base égale à E., La fonction logarithmique en base 10 est parfois appelée fonction logarithmique commune. Il est largement utilisé car notre système de numérotation a une base dix. Les logarithmes naturels sont vus plus souvent dans le calcul.
Il existe deux formules qui permettent de modifier la base d’une fonction logarithmique. Le premier indique ceci: logab = 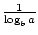 . La formule la plus célèbre et la plus utile pour changer de base est communément appelée le changement de Formule de Base. Il permet de changer la base d’une fonction logarithmique en n’importe quel nombre réel positif ≠1. Il indique que logax =
. La formule la plus célèbre et la plus utile pour changer de base est communément appelée le changement de Formule de Base. Il permet de changer la base d’une fonction logarithmique en n’importe quel nombre réel positif ≠1. Il indique que logax = 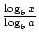 ., Dans ce cas, a, b et x sont tous positifs nombres réels a, b≠1.
., Dans ce cas, a, b et x sont tous positifs nombres réels a, b≠1.
dans la section suivante, nous allons discuter de certaines applications des fonctions exponentielles et logarithmiques.