Dernière mise à jour: 25 janvier 2000
Remarque: Ces notes sont préliminaires et incomplètes et ne sont pas garanties exemptes d’erreurs. Veuillez me faire savoir si vous trouvez des fautes de frappe ou d’autres erreurs.,ke la forme
Y = A·F(K, N)
où
- Y = PIB réel
- a = indice de la productivité globale dans l’économie
- k = quantité d’intrant en capital (mesurée en unités physiques ou en valeur$) dans l’économie
- N = nombre de travailleurs employés dans l’économie
hypothèses concernant la forme
- Le produit marginal du travail, MNP, est positif et décroissant(MPN = dy/DN tenant tout le reste fixe)
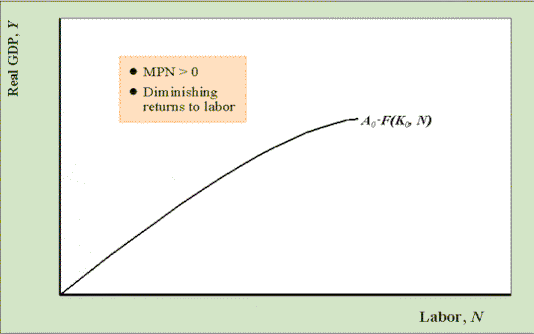
le graphique ci-dessus montre la fonction de production en fonction de n tenant A et K fixes.,
- Le produit Marginal du capital, MPK, est positif et décroissant (MPK = DY/DK tenant tout le reste fixe)
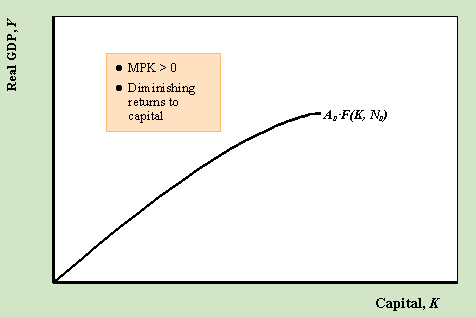
le graphique ci-dessus montre la fonction de production en fonction de K tenant A et N fixe.,
exemple: la constante de Cobb-Douglas retourne à la fonction de production à l’échelle
Y = a·KaN1-a , 0 < a < 1
où
- a = part des revenus perçus par les propriétaires de capital
- 1 – a = part du revenu reçu par le travail
Remarque: Les retours constants à l’échelle signifient que si nous doublons tous les intrants de la fonction de production, la production double exactement., Pour voir que le Cobb-Douglas présente cette propriété, notez que
A·(2K)a(2n)1-A = A·2a21-aKaN1-a = 2a·KaN1-a = 2y
pour les données américaines, provenant des comptes nationaux du revenu et des produits, nous savons que la part du travail dans le revenu est d’environ 0,7 ce qui implique que pour les États-Unis 1-a = 0,7 et a = 0,3.
une hypothèse à moyen terme
la fonction de production montre comment le PIB réel, Y, est déterminé sur une période de temps fixe comme un trimestre ou une année., Au cours de cette période, on suppose que le stock de capital, K, et le niveau de productivité globale, A, sont maintenus fixes alors qu’on suppose que la quantité de travail peut varier. C’est-à-dire qu’au cours de la période de temps supposée, les entreprises de l’économie ne peuvent pas facilement modifier la quantité de capital qu’elles utilisent (c.-à-d. bâtiments, équipement, etc.), mais ils peuvent facilement varier la quantité de travail qu’elles embauchent. De même, on suppose que la productivité ne change pas très rapidement., Compte tenu de ces hypothèses, nous pouvons représenter la fonction de production comme
Y = A0F(K0, N)
où l’indice « 0 » indique que le niveau de productivité est fixé au montant A0 et le niveau de capital est fixé au montant K0. La variable désabonnée, N, est autorisée à varier.
se déplaçant le long des courbes de déplacement
se déplaçant le long de la fonction de production
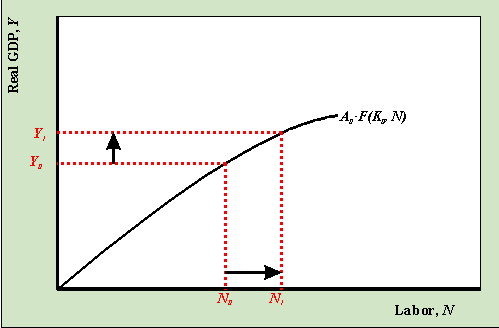
Lorsque N augmente de N0 à N1 la sortie augmente de Y0 à Y1 lorsque nous nous déplaçons le long de la fonction de production.,
déplacement de la fonction de production: augmentation de la productivité
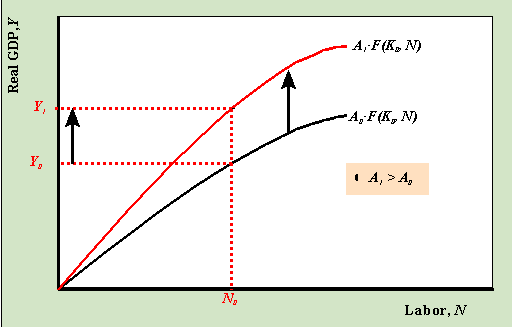
lorsque l’indice de productivité passe de A0 à A1, tout le reste étant fixe, la fonction de production augmente. Ensuite, pour une quantité donnée de travail, N0, la quantité de production produite dans l’économie augmente de Y0 à Y1.
Déplacement de la fonction de production: Une augmentation du stock de capital
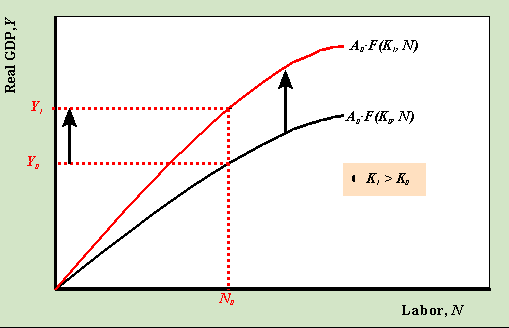
Lorsque le stock de capital augmente de K0 à K1, tenant tout le reste fixe, la fonction de production se déplace jusqu., Ensuite, pour une quantité donnée de travail, N0, la quantité de production produite dans l’économie augmente de Y0 à Y1.