une hypothèse nulle est un énoncé précis sur une population que nous essayons de rejeter avec des données d’échantillon.Nous ne croyons généralement pas que notre hypothèse nulle (ou H0) soit vraie. Cependant, nous avons besoin d’une déclaration exacte comme point de départ pour les tests de signification statistique.
exemples D’hypothèses nulles
souvent-mais pas toujours – l’hypothèse nulle indique qu’il n’y a pas d’association ou de différence entre les variables ou les sous-populations., Ainsi, certaines hypothèses nulles typiques sont:
- La corrélation entre la frustration et l’agression est nulle (analyse de corrélation);
- Le revenu moyen des hommes est similaire à celui des femmes (échantillons indépendants t-test);
- La nationalité n’est (parfaitement) pas liée à la préférence musicale (test d’indépendance du chi carré);
- le revenu moyen de
« Null” Ne Signifie Pas « Zéro”
Un malentendu commun que « null” implique « zéro”. C’est souvent, mais pas toujours le cas., Par exemple, une hypothèse nulle peut également indiquer quela corrélation entre la frustration et l’agressivité est 0.5.No zéro impliqué ici et – bien que quelque peu inhabituel-parfaitement valable.
Le « null » dans” null hypothesis « dérive de”nullify » 5: l’hypothèse nulle est la déclaration que nous essayons de réfuter, qu’elle spécifie ou non un effet nul.
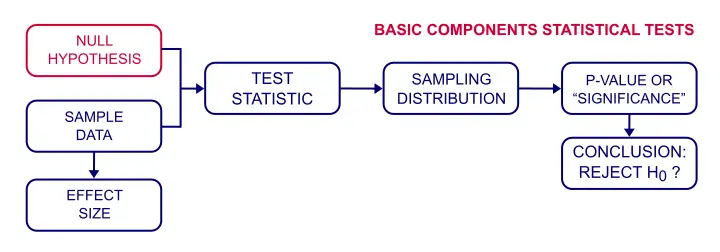
Test D’hypothèse nulle-comment ça marche?
je veux savoir si le bonheur est lié à la richesse chez les Néerlandais. Une approche pour le découvrir consiste à formuler une hypothèse nulle., Comme « lié à » n’est pas précis, nous choisissons l’énoncé opposé comme hypothèse nulle:la corrélation entre richesse et bonheur est nulle chez tous les Néerlandais.Nous allons maintenant essayer de réfuter cette hypothèse afin de démontrer que le bonheur et la richesse sont bien liés.
maintenant, nous ne pouvons pas raisonnablement demander à tous les 17 142 066 néerlandais à quel point ils se sentent généralement heureux.

Nous allons donc demander à un échantillon (disons, 100 personnes) sur leur richesse et leur bonheur. La corrélation entre le bonheur et la richesse s’avère être de 0,25 dans notre échantillon., Maintenant, nous avons un problème: les résultats de l’échantillon ont tendance à différer quelque peu des résultats de la population. Si la corrélation est vraiment zéro dans notre population, nous pouvons trouver un zéro de corrélation dans notre échantillon. Pour illustrer ce point important, jetez un oeil au nuage de points ci-dessous. Il visualise une corrélation nulle entre bonheur et richesse pour une population entière de N = 200.

Maintenant, on dessine un échantillon aléatoire de N = 20 de cette population (les points rouges dans notre précédent nuage de points). Même si notre corrélation de population est nulle, nous avons trouvé un 0 stupéfiant.,82 corrélation dans notre échantillon. La figure ci-dessous illustre cela en omettant toutes les unités non échantillonnées de notre nuage de points précédent.

cela soulève la question de savoir comment nous pouvons jamais dire quoi que ce soit sur notre population si nous n’en avons qu’un petit échantillon. La réponse de base: nous pouvons rarement dire quoi que ce soit avec 100% de certitude. Cependant, nous pouvons en dire beaucoup avec 99%, 95% ou 90% de certitude.
Probabilité
oui, comment cela fonctionne? Eh bien, fondamentalement, certains résultats d’échantillon sont hautement improbables compte tenu de notre hypothèse nulle., Ainsi, la figure ci-dessous montre les probabilités pour différentes corrélations d’échantillon (N = 100) si la corrélation de population est vraiment nulle.

Un ordinateur facilement calculer ces probabilités. Cependant, cela nécessite une taille d’échantillon (100 dans notre cas) et une corrélation de population présumée ρ (0 dans notre cas). C’est pourquoi nous avons besoin d’une hypothèse nulle.
Si nous examinons attentivement cette distribution d’échantillonnage, nous voyons que les corrélations d’échantillon autour de 0 sont les plus probables: il y a une probabilité de 0,68 de trouver une corrélation entre -0,1 et 0,1. Qu’est-ce que ça veut dire?, Eh bien, rappelez-vous que les probabilités peuvent être considérées comme des fréquences relatives. Alors imaginez que nous tirerions 1 000 échantillons au lieu de celui que nous avons. Il en résulterait 1 000 coefficients de corrélation et quelque 680 d’entre eux-une fréquence relative de 0,68 – se situeraient entre -0,1 et 0,1. De même, il y a une probabilité de 0,95 (ou 95%) de trouver une corrélation d’échantillon entre -0,2 et 0,2.
valeurs P
Nous avons trouvé une corrélation d’échantillon de 0,25. Quelle est la probabilité si la corrélation de population est nulle?, La réponse est connue sous le nom de p-value (abréviation de probability value):une p-value est la probabilité de trouver un résultat d’échantillon ou un résultat plus extrême si l’hypothèse nulle est vraie.Compte tenu de notre corrélation de 0,25, « plus extrême” signifie généralement plus grand que 0,25 ou plus petit que -0,25. Nous ne pouvons pas dire de notre graphique mais le tableau sous-jacent nous dit que p ≈ 0.012. Si l’hypothèse nulle est vraie, il y a une probabilité de 1,2% de trouver notre corrélation d’échantillon.
Conclusion?
Si notre corrélation de population est vraiment nulle, alors nous pouvons trouver une corrélation d’échantillon de 0,25 dans un échantillon de N = 100., La probabilité que cela se produise n’est que de 0,012, c’est donc très peu probable. Une conclusion raisonnable est que notre corrélation de population n’était pas nulle après tout.
Conclusion: nous rejetons l’hypothèse nulle. Compte tenu du résultat de notre échantillon, nous ne croyons plus que le bonheur et la richesse ne sont pas liés. Cependant, nous ne pouvons toujours pas l’affirmer avec certitude.
hypothèse nulle – Limitations
Jusqu’à présent, nous avons seulement conclu que la corrélation de population n’est probablement pas nulle. C’est la seule conclusion de notre approche de l’hypothèse nulle et ce n’est pas vraiment intéressant.,
ce que nous voulons vraiment savoir, c’est la corrélation de la population. Notre corrélation d’échantillon de 0,25 semble une estimation raisonnable. Nous appelons un tel nombre unique une estimation ponctuelle.
maintenant, un nouvel échantillon peut arriver avec une corrélation différente. Une question intéressante est de savoir combien nos corrélations d’échantillons fluctueraient au fil des échantillons si nous en tirions beaucoup. La figure ci-dessous montre précisément cela, en supposant notre taille d’échantillon de N = 100 et notre estimation (ponctuelle) de 0,25 pour la corrélation de la population.,

intervalles de confiance
notre résultat de l’échantillon suggère qu’environ 95% de nombreux échantillons devraient présenter une corrélation entre 0,06 et 0,43. Cette plage est connue sous le nom d’intervalle de confiance. Bien que ce ne soit pas précisément correct, c’est plus facilement que la bande passante qui est susceptible d’enfermer la corrélation de population.
Une chose à noter est que l’intervalle de confiance est assez large. Il contient presque une corrélation nulle, exactement l’hypothèse nulle que nous avons rejetée plus tôt.,
Une autre chose à noter est que notre distribution d’échantillonnage et notre intervalle de confiance sont légèrement asymétriques. Ils sont symétriques pour la plupart des autres statistiques (telles que les moyennes ou les coefficients bêta) mais pas les corrélations.