commençons par un exemple simple, disons que nous voulons multiplier (2x-3)3. Ce ne serait pas trop difficile à faire main longue, mais utilisons le théorème binomial de sorte que lorsque vous rencontrez des extensions plus grandes telles que les binômes élevés aux pouvoirs 4, 5, 6,…, vous saurez exactement quoi faire.
pour commencer, vous devez identifier les deux termes de votre binôme (les positions x et y de notre formule ci-dessus) et la puissance (n) à laquelle vous développez le binôme.,
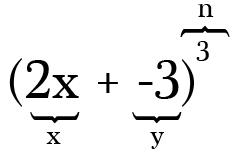
par exemple, Pour développer (2x-3)3, les deux termes sont 2x et de -3 et de la puissance, ou la valeur de n, est 3. Notez que chaque fois que vous avez une soustraction dans votre binôme, il est oh si important de se rappeler d’inclure le moins comme symbole négatif sur le terme d’accompagnement.
la chose merveilleuse à propos du théorème binomial est qu’il nous permet de trouver le polynôme étendu sans multiplier un tas de binômes ensemble. Très soigné, non?, Il s’avère que le nombre de termes dans votre polynôme étendu sera toujours un de plus que la puissance que vous développez. Cela signifie que nous allons créer un polynôme avec 4 Termes puisque la puissance dans cet exemple est 3.
chaque terme aura un (2x) et (-3) ainsi que la formule « n choisissez k” où n=3. Vous pouvez aller de l’avant et l’écrire 4 fois, une pour chaque terme, en laissant la valeur k dans « n choisissez k” et les pouvoirs vides pour le moment.
ensuite, vous voudrez remplir les k-valeurs et les puissances. Ici, vous pouvez suivre la formule de sommation, en augmentant la puissance pour chaque terme., Mais il est assez facile de suivre les tendances.
Les k valeurs dans « n choisissez k”, commenceront par k=0 et augmenteront de 1 à chaque terme. Le dernier terme devrait se terminer avec n égal à k, dans ce cas n=3 et k=3.
Ensuite, nous devons ajouter les pouvoirs sur (2x) et (-3).
la mise sous tension (2x) commencera par la valeur n, donc dans ce cas 3, et diminuera de 1 à chaque terme, jusqu’à ce que vous arriviez à zéro. La mise sous tension (-3) commencera par zéro et augmentera d’un à chaque fois jusqu’à ce que vous arriviez à n, ou 3 dans ce problème.,

Parce que toute valeur élevé à la puissance nulle est égale à 1, vous pouvez simplifier les termes ayant le pouvoir de zéro.

Ensuite aller de l’avant et appliquer les pouvoirs et les simplifier dans la mesure du possible.,

La le Triangle de Pascal Raccourci

La dernière partie est de résoudre les combinaisons de formule. La façon évidente de le faire est d’appliquer la formule de combinaisons pour chaque problème. Mais nous allons prendre un joli petit raccourci ici en utilisant le Triangle de Pascal.
Le Triangle de Pascal est un triangle simple mais puissant formé en créant un triangle avec trois 1 pour commencer., Pour chaque ligne par la suite, vous écrivez simplement 1 aux deux extrémités et trouvez le(S) nombre (s) du milieu en ajoutant les deux valeurs directement au-dessus.

Maintenant, voici la bonne partie. Caché dans le Triangle de Pascal sont toutes les réponses à tout « n choisir k »! C’est comme un petit cheatsheet secret!
le diagramme ci-dessous vous montre où se trouvent les « n choose k” cachés.,

Pour notre problème, nous devons trouver des solutions pour: 3 choisissez 0, 3 choisir 1, 3 choisissez 2, et 3 choisissez 3. Qui est toutes les valeurs de la 4ème ligne. Donc, tout ce que nous devons faire est de regarder la 4ème rangée du Triangle de Pascal et de faire correspondre les réponses.
La 4ème ligne a les valeurs: 1, 3, 3, 1. Donc, je vais juste remplacer dans les réponses pour nos N choisir K.,

Enfin, tout ce que vous devez faire est de multiplier et de simplifier chaque terme vers le bas à sa forme la plus simple. N’oubliez pas de vérifier votre réponse finale pour vous assurer que les pouvoirs sur chaque terme ajoutent toujours au degré de votre binôme d’origine! Croyez-moi, il est incroyablement facile de faire une erreur de transcription dans ce type de problème 😉
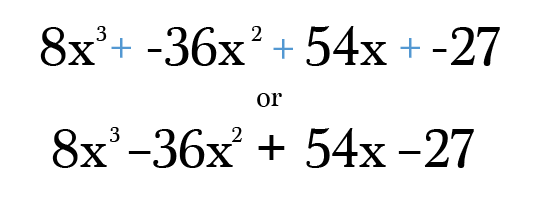
Besoin d’un autre exemple?,
dans la vidéo ci – dessus, je vous montre comment utiliser le théorème Binomial pour développer le binôme (x-3y)⁵. De plus, je vous montre quelques astuces supplémentaires pour rester organisé et quelques vérifications rapides que vous pouvez utiliser pour identifier facilement les erreurs courantes.
Merci pour la lecture!
❤ restez connecté ❤
Restez à jour avec tout ce que Math Hacks fait!