sur ces pages, nous examinons quelques concepts intéressants, nous examinons l’espace incurvé: ce que signifie l’espace incurvé, comment nous pouvons dire si un espace est incurvé de l’intérieur ou de l’extérieur.
nous regardons comment nous pouvons intégrer un type d’espace à l’intérieur d’un autre et voir que nous pouvons cartographier entre différents espaces de différentes manières.
nous examinons également la compacification et comment nous pouvons représenter des vecteurs infiniment grands et infiniment petits dans nos espaces de manière à ne pas conduire à des singularités et à d’autres problèmes.,
ces concepts s’avèrent utiles, même lorsque nous travaillons avec un espace plat, nous trouverons des moyens de représenter des vecteurs et des plans qui ne passent pas par l’origine. Cela nous donne des moyens de représenter les rotations et les traductions en une seule opération.
L’autre application est l’espace-temps relativiste.
géométrie Rienmannienne
en Géométrie Rienmannienne, l’espace peut se courber à différents endroits (voir manifolds) nous examinons ici les géométries où la courbe de l’espace est constante.,
Eulidean Géométrie
espace
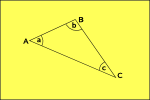
la Géométrie Hyperbolique
l’espace des courbes vers l’extérieur
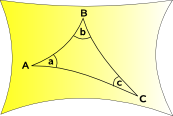
la Géométrie Sphérique et Géométrie Elliptique
l’espace des courbes vers l’intérieur
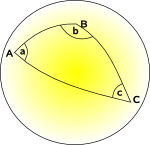
Dans une courbe (Non-Euclidienne, la géométrie nous ne pouvons pas trouver un ensemble de coordonnées qui sont mutuellement perpendiculaires, où la ligne de coordonnées sont tous parallèles les uns aux autres et où chaque carré de la grille a la même région., Nous pouvons éventuellement trouver un système de coordonnées où nous pouvons faire certains d’entre eux, mais pas tous.
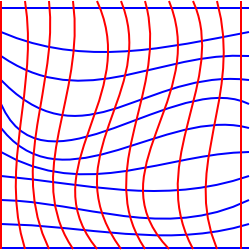
Ce diagramme essaie d’illustrer cette situation en 2 dimensions, bien que ce soit un peu trompeur, car nous l’avons dessiné sur un plan pour pouvoir dessiner des coordonnées rectangulaires.
pour essayer d’illustrer une situation où cela est impossible, nous pourrions penser à un plan bidimensionnel qui a été étiré dans la troisième dimension.,

dans cette situation, nous pouvons choisir des coordonnées qui forment une grille rectangulaire lorsqu’elles sont projetées sur un plan horizontal, cependant, pour une personne vivant dans la surface, certains des carrés de la grille sembleront avoir une surface plus grande que d’autres et les lignes de la grille peuvent ne pas Il n’y a pas de système de coordonnées à deux dimensions qui préservera les lignes parallèles, les angles et les zones en même temps.,
un exemple similaire est d’essayer de cartographier la surface de la terre, nous pouvons utiliser des lignes de latitude et de longitude mais les lignes de longitude se rapprochent plus près des pôles.
dans ces cas, nous pourrions travailler en termes de coordonnées 3 dimensions et c’est une approche que nous adopterons avec certains types de géométries non euclidiennes. Il est souvent possible d’intégrer une géométrie particulière dans une géométrie de dimension supérieure afin de la rendre plus euclidienne.,
C’est parfois le cas, que, lorsque nous regardons une géométrie à grande échelle qu’il est non-Euclidienne, mais si l’on regarde sur une plus petite échelle, puis il se rapproche d’une géométrie Euclidienne. Pour ce faire, nous devons trouver un système de coordonnées où les angles sont préservés en chaque point, c’est-à-dire que les lignes de coordonnées horizontales et verticales doivent toujours se croiser à 90° même si les lignes ne sont pas droites. Ceci est connu comme une géométrie conforme. Dans ce type de géométrie, nous pouvons au moins définir un système de coordonnées local.,
lié à cela est de savoir si la géométrie peut être différenciée et intégrée, une condition pour cela est qu’elle doit être bien comportée et ne pas avoir de sauts soudains, etc. Certaines géométries et systèmes de coordonnées peuvent être bien comportés à certains endroits, mais ont des singularités, etc.
pour une discussion sur la façon dont la courbure est mesurée, voir cette page.
Mathématiques
Comment faire face à des géométries où nous ne pouvons pas utiliser toutes les règles qui s’appliquent à géométrie euclidienne?,
Une approche consiste à utiliser la notation tensorielle, cela fournit des conventions et une notation qui nous aident à basculer entre différents systèmes de coordonnées. Un système de coordonnées orthogonales, local à n’importe quel point, peut être défini en utilisant des vecteurs de base qui sont des tangentes aux lignes de coordonnées.,Collecteur
voir la page
Relation entre Hyperbolique et Minkowski Géométries
| Géométrie de Minkowski | Géométrie Hyperbolique | |
| point | événement dans l’espace-temps | particule en mouvement uniforme |
| distance entre deux points | espace-intervalle de temps entre deux événements | vitesse relative entre les deux particules |
la Terminologie
nous nous intéressons Ici à la terminologie comme les géométries, des espaces, des modèles, des projections et des transformations., C’est assez difficile lorsque nous commençons à traiter des géométries non euclidiennes car nous utilisons une terminologie similaire à celle à laquelle nous sommes habitués dans l’espace euclidien conventionnel, mais les Termes peuvent avoir des propriétés légèrement différentes.,essayez
Géométrie Elliptique
Modèles
voici quelques Exemples:
- Tige demi-plan de modèle
- disque de Poincaré modèle
- modèle Projectif
- Conforme du modèle
les Projections
Projection Stéréographique
Transforme
Invariant
voici quelques Exemples:
- Möbius Transformer
- Lorentz Transformer
Parallèle Postulat
Si nous retirons le parallèle postulat de l’Espace Euclidien.,
cela conduit à:
- le postulat parallèle est faux
- Les angles d’un triangle ne s’ajoutent pas à π
- pour une forme d’une taille donnée, il n’existe en général pas de forme similaire d’une taille plus grande.,ctive
conformationnelle (disque de Poincaré ) les lignes droites – les géodésiques les segments de cercles angle préserver plus angles internes d’un triangle π-(α+β+γ)=CΔ la distance entre deux points avec