automates Finis peuvent avoir des sorties correspondant à chaque transition. Il existe deux types de machines à états finis qui génèrent une sortie −
- Mealy Machine
- Moore Machine
Mealy Machine
Une machine Mealy est une FSM dont la sortie dépend de l’état actuel ainsi que de l’entrée actuelle.,
Il peut être décrit par un 6 n-uplet (Q, ∑, O, δ, X, t0) où −
-
Q est un ensemble fini d’états.
-
∑ est un ensemble fini de symboles appelés » l’entrée de l’alphabet.
-
O est un ensemble fini de symboles appelée la sortie de l’alphabet.
-
δ est l’entrée de la transition de la fonction où δ: Q × ∑ → Q
-
X est la transition de sortie de la fonction X: Q × ∑ → O
-
q0 est l’état initial d’où les données d’entrée sont traitées (q0 ∈ Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
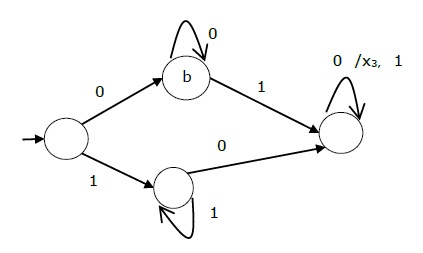
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
Une machine de Moore peut être décrite par un 6 n-uplet (Q, ∑, O, δ, X, t0) où −
-
Q est un ensemble fini d’états.
-
∑ est un ensemble fini de symboles appelés » l’entrée de l’alphabet.
-
O est un ensemble fini de symboles appelée la sortie de l’alphabet.
-
δ est l’entrée de la transition de la fonction où δ: Q × ∑ → Q
-
X est la transition de sortie de la fonction X: Q → O
-
q0 est l’état initial d’où les données d’entrée sont traitées (q0 ∈ Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
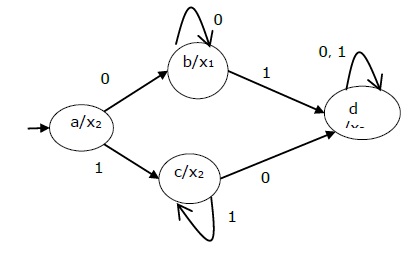
Mealy Machine vs., Machine Moore
Le tableau suivant met en évidence les points qui différencient une Machine Mealy d’une Machine Moore.
Machine de Mealy Machine de Moore Sortie dépend à la fois sur l’état actuel et l’entrée actuelle Sortie dépend uniquement à l’état actuel. Généralement, il a moins d’états que la machine de Moore. Généralement, il a plus d’états que Mealy Machine., La valeur de la fonction de sortie est une fonction des transitions et des changements, lorsque l’entrée logique sur l’état présent est fait. la valeur de la fonction de sortie est une fonction de l’état actuel et des changements aux bords de l’horloge, chaque fois que des changements d’état se produisent. Farineuse machines de réagir plus rapidement aux entrées. Ils réagissent généralement dans le même cycle d’horloge. dans les machines Moore, plus de logique est nécessaire pour décoder les sorties, ce qui entraîne plus de retards de circuit. Ils réagissent généralement un cycle d’horloge plus tard., Machine de Moore à la machine Mealy
algorithme 4
entrée − Machine Moore
sortie − Machine Mealy
Étape 1 − Prenez un format de table de transition de machine mealy vierge.
Étape 2-Copiez tous les états de transition de la machine Moore dans ce format de table.
Étape 3-Vérifiez les États présents et leurs sorties correspondantes dans la table D’état de la machine Moore; si pour un État la sortie Qi est m, copiez-la dans les colonnes de sortie de la table D’état de la Machine Mealy partout où Qi apparaît dans l’état suivant.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
Étape 2 – si toutes les sorties de Qi sont identiques, copiez L’État Qi. Si elle a n sorties distinctes, briser Qi en n États comme Qin où n = 0, 1, 2…….
Étape 3-si la sortie de l’état initial est 1, Insérez un nouvel état initial au début qui donne la sortie 0.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Mais les États » b » et » c » produisent des sorties différentes (1 et 0). Donc, nous divisons b en b0, b1 et c en c0, c1., »>
Output