
vous êtes-vous déjà demandé comment il peut neiger au-dessus du point de congélation? Eh bien, l’explication naïve est qu’il faut simplement du temps pour que les flocons de neige fondent une fois qu’ils pénètrent dans l’air au-dessus du point de congélation, alors qu’ils descendent vers le sol. C’est bien sûr la raison pour laquelle la grêle peut tomber par temps chaud. Simplement, les pierres de grêle tombent vite, trop vite pour laisser l’air chaud faire fondre la grêle. Ce n’est pas la principale explication, cependant, pour pourquoi il peut neiger quand il est au-dessus du point de congélation.,
D’après la figure ci – dessous, il est évident qu’il existe une dépendance claire à l’humidité-plus il est sec, plus il peut être chaud lorsqu’il neige. Cela implique que le facteur principal, au moins dans des conditions sèches, a à voir avec l’humidité. Et ce facteur est due à l’évaporation. Plus précisément, à mesure que les flocons de neige descendent, ils s’évaporent. Ce processus prend de la chaleur et garde les flocons au froid.
ainsi, si nous voulons calculer la température maximale, nous devons estimer le bilan thermique net du flocon. Tout d’abord, lorsque les flocons se déplacent dans un environnement chaud, ils gagnent de la chaleur de l’environnement par conduction., Deuxièmement, la chaleur est utilisée pour évaporer les flocons, les refroidissant ainsi. Si le « dissipateur » de chaleur par évaporation est plus grand que la conduction thermique, les flocons resteront gelés.
Il s’avère que cela peut être facilement calculé. Non, il n’est pas simple de calculer la conduction thermique ou la chaleur d’évaporation, mais le rapport l’est, car divers facteurs géométriques inconnus s’annulent.
Si vous ne vous souciez pas du calcul (parce que vous n’êtes pas un monstre de science), vous pouvez simplement visiter la page de la calculatrice.
Si vous vous souciez, voici la dérivation., Supposons que l’écoulement autour des flocons soit tel qu’une couche limite de largeur d se forme autour d’elle. Le total des flux de chaleur $F_H$ à l’écaille (p. ex., J/sec en MKS) sera donnée par la transformée de Fourier de la loi:
où $\kappa$ est la chaleur le coefficient de diffusion de l’air (p. ex., m2/s dans le système MKS), c est la capacité calorifique de l’air (J/kg dans MKS), A est la surface de la couche limite autour de l’écaille, tandis que ∆ T est la différence de température entre l’écaille et de l’environnement.,
de même, on peut utiliser la loi de Fick pour obtenir la diffusion de la vapeur d’eau du flocon (où la température est proche du point de congélation, et l’humidité relative est de 100%), vers le milieu environnant, où la température est plus élevée et l’humidité relative plus faible:
ici, D est le coefficient de diffusion de l’eau (par exemple, m2/s en MKS) et ρ est la densité de vapeur d’eau (kg/m3 en MKS).,
la glace qui s’évapore nécessite de la chaleur, ainsi, s’il y a un flux massique de vapeur D’eau de Φ provenant du flocon, il faudrait de la chaleur à une vitesse de $F_w = \epsilon \Phi where où \ \ epsilon is est la chaleur de vaporisation de la glace (J/kg en MKS).
la température la plus élevée au-dessus de laquelle le flocon de neige fond est la température pour laquelle les deux flux de chaleur sont égaux:
notez que la géométrie du flux autour du flocon s’annule, car les deux flux de chaleur dépendent de D et a de la même manière., Ce serait également le cas si la couche limite autour du flocon est complexe de telle sorte que d dépend réellement de la direction. Par conséquent,
où \ \ rho_{SAT} is est la densité de vapeur d’eau de saturation.
brancher les nombres (qui peuvent être trouvés par exemple dans le manuel CRC de chimie et de physique), les résultats avec une équation implicite pour la températureparce que la densité de vapeur d’eau de saturation dépend aussi de la température., Nous pouvons simplifier les choses si nous demandons plutôt Quelle est l’humidité relative nécessaire pour garder le flocon congelé à une température donnée. C’est:
où t t_c is est la température en degré Celsius.
Cette fonction peut être vue dans la figure ci-dessous, avec les données de Matsuo et Sasyo, 1981. Comme on peut le voir sur la figure, le graphique calculé est à peu près la limite inférieure en dessous de laquelle il n’y a aucune pluie. À des températures plus chaudes, il y a un mélange., Jusqu’à environ 1°C au-dessus de la ligne de non fusion, il y a principalement de la neige alors qu’entre environ 1°C et 2°C au-dessus de la ligne, il y a principalement de la pluie, mais de la neige est possible. Ces événements pourraient être dus à des effets supplémentaires, tels que de forts courants descendants, le temps nécessaire pour faire fondre la neige, etc.
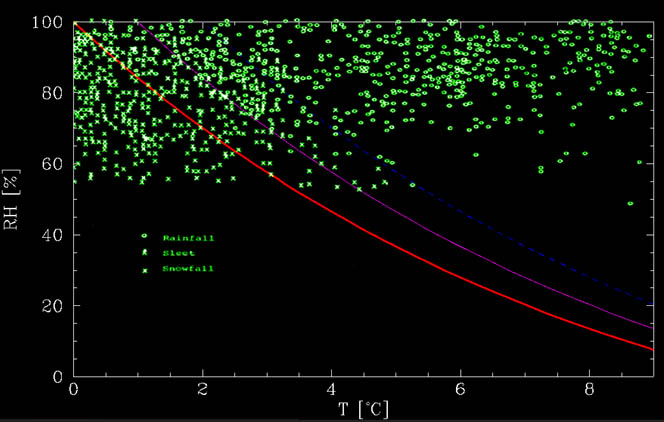
ainsi, si nous souhaitons observer de la neige par temps chaud, des conditions très sèches sont nécessaires. Par exemple, si l’humidité du sol n’est que d’environ 20% (très rare, car s’il y a des précipitations, l’atmosphère est généralement humide!) puis il pourrait neiger à 8°C (ou 46°F pour les utilisateurs Anglais).,
Une autre exigence est que nulle part le long de la descente, l’air ne dépasse la ligne sans fusion. Si c’est le cas, le flocon fondra bien sûr.
Si la température dépasse le point de congélation, il n’y a aucun paramètre avec lequel le type de précipitation peut être déterminé avec certitude. Tout ce que nous pouvons prédire est la probabilité que la neige va tomber. Cela peut être fait en utilisant les résultats de Häggmark et Ivarsson (1997), uniquement corrigés pour utiliser le bulbe congelé et non la température du bulbe humide.
la ligne de fond est une calculatrice avec laquelle la probabilité de neige peut être estimée.,