résoudre des équations numériquement

trouver toutes les racines d’une fonction polynomiale

utiliser vpasolve pour trouver toutes les solutions à la fonction f(x)=6×7-2×6+3×3-8.

syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)

vpasolve retourne sept racines de la fonction, comme prévu, parce que la fonction est un polynôme de degré de sept.,

trouver des zéros d’une fonction non Polynomique en utilisant des plages de recherche et des Points de départ

un tracé de la fonction f(x)=e(x / 7)cos(2x) révèle des zéros périodiques, avec des pentes croissantes aux points zéro à mesure que x augmente.

syms xh = fplot(exp(x/7)*cos(2*x),);grid on

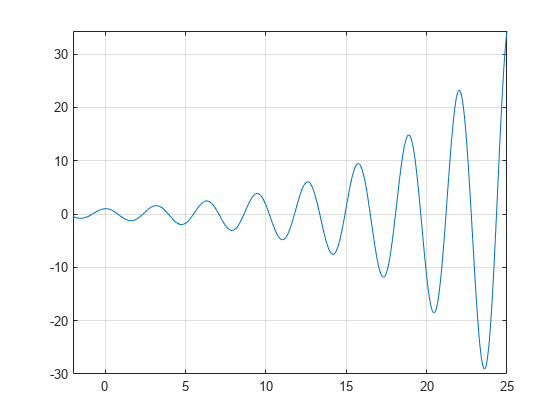
Utiliser vpasolve pour trouver un zéro de la fonction f. Notez que vpasolve ne renvoie qu’une seule solution d’une équation non polynomiale, même si plusieurs solutions existent., On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3 vpasolve(f,x,'Random',true)end

ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')

ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')

ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')

To find a zero close to x=10, set the starting point to 10.,

vpasolve(f,x,10)

ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')

Pour trouver le zéro proche de x=1000, définissez le point de départ de 1000.

vpasolve(f,x,1000)

ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')

Pour trouver le zéro de l’ordre de 15≤x≤25, définissez la plage de recherche de: .,

vpasolve(f,x,)

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

Pour trouver plusieurs zéros dans la gamme , vous ne pouvez pas appeler vpasolve à plusieurs reprises parce qu’il renvoie le même résultat à chaque appel, comme montré précédemment. Au lieu de cela, définissez la plage de recherche et définissez 'Random' sur true.,

for k = 1:3 vpasolve(f,x,,'Random',true)end

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')

Car 'Random' sélectionne les points de départ au hasard, la même solution peut être trouvée sur les appels successifs.,

Trouver Tous les Zéros dans la bande de Recherche

Créez une fonction: findzeros pour trouver systématiquement tous les zéros de f dans une plage de recherche, l’intérieur d’une certaine tolérance à l’erreur. La fonction commence par la plage de recherche d’entrée et appelle vpasolve pour trouver un zéro. Ensuite, il divise la plage de recherche en deux autour de la valeur zéro et s’appelle récursivement avec les nouvelles plages de recherche comme entrées pour trouver plus de zéros.

La fonction est expliquée par l’article ici.,

Déclarer la fonction avec les trois entrées et une sortie. La première entrée est la fonction, la deuxième entrée est de la gamme, et la troisième entrée vous permet de spécifier l’erreur entre zéro et les plus élevés et les plus faibles issus.

function sol = findzeros(f,range,err)

Si vous ne spécifiez pas l’argument optionnel pour la tolérance à l’erreur, findzeros configure err de 0.001.

if nargin < 2 err = 1e-3;end

Trouver un zéro dans la plage de recherche à l’aide de vpasolve.,

sol = vpasolve(f,range);

Si vpasolve ne trouve pas un zéro, la sortie.

if(isempty(sol)) return

Si vpasolve trouve un zéro, split la plage de recherche en deux plages de recherche ci-dessus et au-dessous du zéro.

else lowLimit = sol-err; highLimit = sol+err;

Appel findzeros avec le bas de gamme de recherche. Si findzeros renvoie des zéros, copiez les valeurs dans le tableau de solutions et triez-les.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end

Appel findzeros avec la plus grande plage de recherche., Si findzeros renvoie des zéros, copiez les valeurs dans le tableau de solutions et triez-les.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend

l’ensemble de La fonction findzeros est comme suit. Enregistrez cette fonction sous findzeros.m dans le dossier actuel.

syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'

Obtenir des Solutions de Précision Arbitraire

Utiliser digits pour régler la précision de la solutions retournées par vpasolve., Par défaut, vpasolve renvoie les solutions à une précision de 32 chiffres significatifs.

f = exp(x/7)*cos(2*x);vpasolve(f)

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

Utiliser digits pour augmenter la précision de 64 chiffres significatifs. Lorsque vous modifiez digits, assurez-vous d’enregistrer sa valeur actuelle afin de pouvoir la restaurer.,

digitsOld = digits;digits(64)vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')

Ensuite, modifier la précision des solutions à 16 chiffres significatifs.

digits(16)

Résoudre Multivariée Équations à l’Aide de Plages de Recherche

Considérons le système suivant d’équations.

Un complot des équations pour 0≤x≤2,5 et 0≤x≤2.5 montre que les trois surfaces se coupent en deux points., Pour mieux visualiser le tracé, utilisez view. Pour mettre à l’échelle les valeurs de la carte de couleurs, utilisez caxis.

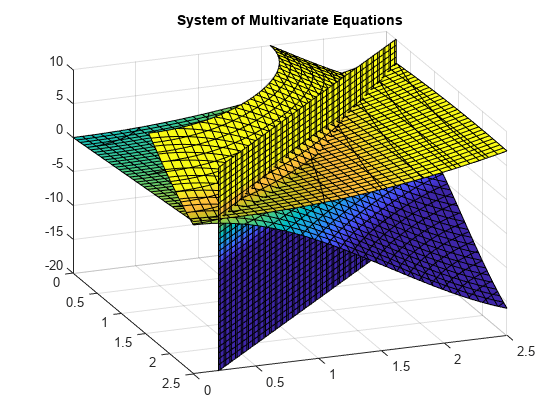
Utiliser vpasolve pour trouver le point où les surfaces se coupent. La fonction vpasolve renvoie une structure. Pour accéder aux valeursx -,y – Etz-de la solution, indexez-les dans la structure.,

sol = vpasolve(equations);

À la recherche d’une région de l’espace des solutions, spécifier des plages de recherche pour les variables. Si vous spécifiez les plages 0≤x≤1.5 et 1.5≤y≤2.5, alors vpasolve la fonction recherche la zone délimitée affichée.

Utiliser vpasolve pour trouver une solution à cette plage de recherche. Pour omettre une plage de recherche pour z, définissez la troisième plage de recherche sur .,

vars = ;range = ;sol = vpasolve(equations, vars, range);

Pour trouver de multiples solutions, définir la balise 'Random' option true. Cela fait quevpasolve utilise des points de départ aléatoires lors d’exécutions successives. L’option'Random' peut être utilisée conjointement avec des plages de recherche pour faire en sorte quevpasolve utilise des points de départ aléatoires dans une plage de recherche. Parce que 'Random' sélectionne les points de départ de manière aléatoire, la même solution peut être trouvée lors d’appels successifs., Appelez vpasolve à plusieurs reprises pour vous assurer de trouver les deux solutions.

Tracer les équations. Superposez les solutions sous forme de nuage de points avec des marqueurs jaunes X en utilisant scatter3. Pour mieux visualiser le tracé, rendez deux des surfaces transparentes en utilisant alpha. Mettez la palette de couleurs à l’échelle en utilisant caxis et modifiez la perspective en utilisant view.

vpasolve trouve des solutions à l’intersection des surfaces formé par les équations comme indiqué.,

Lastly, restore the old value of digits for further calculations.

digits(digitsOld)