sections transversales

propriétés des aires

centroïde

le centroïde d’une forme représente le point autour duquel l’aire de la section est répartie uniformément. Si l’aire est doublement symétrique autour de deux axes orthogonaux, le centroïde se trouve à l’intersection de ces axes. Si l’aire est symétrique autour d’un seul axe, alors le centroïde se trouve quelque part le long de cet axe (l’autre coordonnée devra être calculée)., Si l’emplacement exact du centre de gravité ne peut pas être déterminée par l’inspection, il peut être calculé par:

où dA représente le domaine de l’infiniment petit élément de A est l’aire totale de la section transversale, et x et y sont les coordonnées de l’élément de dA par rapport à l’axe de l’intérêt.,

Les emplacements centroïdes des sections transversales communes sont bien documentés, il n’est donc généralement pas nécessaire de calculer l’emplacement avec les équations ci-dessus., des formes de base dont centroidal emplacements sont connus à l’égard de certains point de référence, puis la centroidal emplacement du composite de la section transversale peut être calculée comme suit:

où xc,i et yc,i sont les coordonnées rectangulaires du centroidal emplacement de la ie section concernant le point de référence, et l’Ia est la zone de la ie section.,

distance Centroidale

la distance centroidale, c, est la distance entre le centroïde d’une section transversale et la fibre extrême., Le centroidal distance dans la direction y pour une section transversale rectangulaire est montré dans la figure ci-dessous:

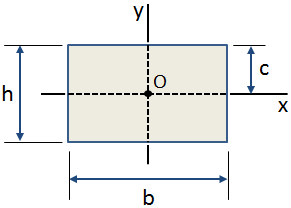
utilisations Courantes centroidal distance incluent:

• le calcul de la contrainte de flexion maximale dans une section transversale
• le calcul de la valeur du premier moment de zone, Q, au-dessus d’un point dans la section transversale de déterminer la contrainte de cisaillement à ce point

Premier Moment de Domaine

Le premier moment d’une zone par rapport à un axe d’intérêt est calculé comme suit:

Qx = ∫ y dA

Qy = ∫ x dA

où Qx est le premier moment autour de l’axe x et Qy est le premier moment autour de l’axe des ordonnées.,Si la zone est composée d’une collection de formes de base dont centroidal emplacements sont connus par rapport à l’axe de l’intérêt, le premier moment de la composite de la zone peut être calculée comme suit:

Notez que le premier instant de la zone est utilisée lors du calcul du centre de gravité d’une section à l’égard de certains de l’origine (comme expliqué précédemment)., Le premier moment est également utilisé lors du calcul de la valeur de la contrainte de cisaillement en un point particulier de la section transversale. Dans ce cas, le premier moment est calculé pour une zone qui constitue une partie plus petite de la section transversale, où la zone est délimitée par le point d’intérêt et la fibre extrême (supérieure ou inférieure) de la section transversale. Le premier moment est calculé autour d’un axe qui traverse le centroïde de la section transversale.,

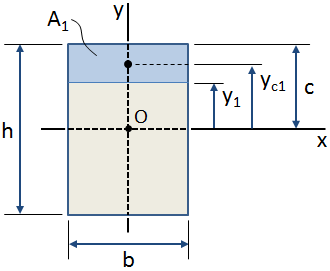
Dans la figure ci-dessus, le ombrées en bleu est la région d’intérêt dans l’ensemble de la section transversale.,nt de cette zone par rapport à l’axe des abscisses (qui traverse le centroïde de section transversale, Point O sur la figure ci-dessus) est calculé comme suit:

Si l’emplacement centroïde de la zone d’intérêt est connu, alors le premier moment l’aire par rapport à l’axe peut être calculée comme (voir la figure ci-dessus):

Il convient de noter que le premier moment d’une aire sera positif ou négatif en fonction de la position de la position de la zone par rapport à l’axe d’intérêt., Par conséquent, le premier moment de toute la surface d’une section transversale par rapport à son propre centroïde sera nul.

Moment D’inertie de la zone

le deuxième moment de la zone, plus communément appelé moment d’inertie, I, d’une section transversale est une indication de la capacité d’un élément structurel à résister à la flexion.,(Note 1) Ix et Iy sont les moments d’inertie autour des axes x et y, respectivement, et sont calculés par:

Ix = Y Y2 dA

Iy = ∫ x2 dA

où x et y sont les coordonnées de par rapport à l’axe D’intérêt.

Le plus souvent, les moments d’inertie sont calculés par rapport au centroïde de la section. Dans ce cas, ils sont appelés moments d’inertie centroïdes et sont notés Icx pour l’inertie autour de l’axe des abscisses et Icy pour l’inertie autour de l’axe des ordonnées.,

Les moments d’inertie des sections transversales communes sont bien documentés, il n’est donc généralement pas nécessaire de les calculer avec les équations ci-dessus. Les propriétés de plusieurs sections communes sont données à la fin de cette page.

Si une section est composée d’une collection de formes de base dont les centroïdes sont tous coïncident, alors le moment d’inertie de la section composite est simplement la somme des moments d’inertie. Un exemple de ceci est une poutre caisson qui se compose de deux sections rectangulaires, comme indiqué ci-dessous., Dans ce cas, la section externe a « positif » zone à l’intérieur de la section a « négatif », afin que le composite moment d’inertie est la soustraction du moment d’inertie de la section intérieure de la partie extérieure.

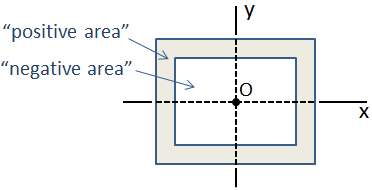
dans le cas d’une section transversale composite plus compliquée dans laquelle les emplacements centroïdes ne coïncident pas, le moment d’inertie peut être calculé en utilisant le théorème de l’axe parallèle.

Il est important de ne pas confondre le moment d’inertie d’une zone avec le moment d’inertie d’un corps solide., Le moment d’inertie de la zone indique la résistance d’une section transversale à la flexion, tandis que le moment d’inertie de la masse indique la résistance d’un corps à la rotation.,

théorème de L’axe parallèle

Si le moment d’inertie d’une section transversale autour d’un axe centroidal est connu, alors le théorème de l’axe parallèle peut être utilisé pour calculer le moment d’inertie autour d’un axe parallèle quelconque:

où Ic est axe centroidal et l’axe parallèle, et a est l’aire de la section transversale.,

Si une section transversale est composée d’une collection de formes de base dont les moments d’inertie centroïdes sont connus avec les distances des centroïdes à un point de référence, alors le théorème de l’axe parallèle peut être utilisé pour calculer le moment d’inertie de la section transversale composite.

Par exemple, un faisceau en I peut être approximé par 3 rectangles, comme indiqué ci-dessous. Comme cette section composite est symétrique par rapport aux axes x et y, le centroïde de la section peut être localisé par inspection à l’intersection de ces axes. Le centroïde est situé à L’origine, O, sur la figure.,

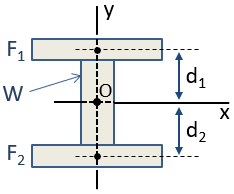
Le moment d’inertie de la section composite peut être calculé à l’aide de l’axe parallèle théorème. Le moment d’inertie centroïdal de la section autour de L’axe des abscisses, Icx, est calculé comme suit:

où les Termes Icx sont les moments d’inertie des sections individuelles autour de leurs propres centroïdes dans l’orientation de l’axe des abscisses, les Termes d sont les distances des centroïdes de section individuelle au centroïde de section composite, et les Termes A sont les aires des sections individuelles. Comme le centroïde de la section W et le centroïde de la section composite coïncident, d est nul pour cette section et il n’y a donc pas de terme Ad2.,

Il est important de noter l’implication du théorème de l’axe parallèle que lorsqu’une section individuelle s’éloigne du centroïde de la section composite, la contribution de cette section au moment d’inertie de la section composite augmente d’un facteur d2. Par conséquent, si l’intention est d’augmenter le moment d’inertie d’une section sur un axe particulier, il est plus efficace pour localiser la zone à partir de cet axe que possible. Ceci explique la forme d’une poutre en I., Les brides sont les principaux contributeurs au moment d’inertie, et la bande sert à séparer les brides de l’axe de flexion. La bande doit cependant maintenir une certaine épaisseur pour éviter le flambage et parce que la bande prend une partie importante de la contrainte de cisaillement dans la section.

le Moment d’Inertie Polaire

Le moment d’inertie polaire, j’, d’une section transversale est une indication d’un élément de construction de la capacité de résister à la torsion autour d’un axe perpendiculaire à la section., Le moment d’inertie polaire d’une section par rapport à un axe peut être calculé par:

où x et y sont les coordonnées de l’élément dA par rapport à l’axe d’intérêt, et r est la distance entre l’élément dA et l’axe d’intérêt.,

bien que le moment d’inertie polaire puisse être calculé en utilisant l’équation ci-dessus, il est généralement plus pratique de le calculer en utilisant le théorème de l’axe perpendiculaire, qui stipule que le moment d’inertie polaire d’une zone est la somme des moments d’inertie autour de deux axes orthogonaux quelconques qui passent par l’axe d’intérêt:

Le plus centroïde de la section transversale.,

module de Section

la contrainte de flexion maximale dans une poutre est calculée comme σb = Mc / Ic, où c est la distance entre l’axe neutre et la fibre extrême, ici est le moment d’inertie centroïde et M est le moment de flexion. Le module de section combine les termes c et Ic dans l’équation de contrainte de flexion:

En utilisant le module de section, la contrainte de flexion est calculée comme σb = M / s. l’utilité du module de section est qu’il caractérise la résistance à la flexion d’une section transversale en un seul terme., Cela permet d’optimiser la section transversale d’une poutre pour résister à la flexion en maximisant un seul paramètre.

rayon de giration

Le rayon de giration représente la distance du centroïde d’une section à laquelle toute la zone pourrait être concentrée sans avoir d’effet sur le moment d’inertie.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

propriétés des sections communes

Le tableau ci-dessous donne les propriétés des sections communes. Des tableaux plus détaillés peuvent être trouvés dans les références énumérées.

Les propriétés calculées dans le tableau comprennent l’Aire, le moment d’inertie centroidal, le module de section et le rayon de giration.,

notes

Note 1: déviation d’une poutre

La déviation d’une poutre en flexion est déterminée par le moment d’inertie de la section transversale, la longueur de la poutre et le module élastique du matériau. Plus de détails sont donnés dans cette discussion sur la déviation du faisceau.