kezdjük egy egyszerű példával, mondjuk, hogy szaporodni akarunk (2x-3)3. Ez nem lenne túl nehéz csinálni hosszú kéz, de használjuk a binomiális tétel úgy, hogy ha találkozik nagyobb bővítések, mint a binomials emelt a 4, 5, 6, … hatáskörök akkor pontosan tudja, mit kell tennie.
az induláshoz meg kell határoznia a két kifejezést a binomiális (a fenti képlet x és y pozíciói), valamint a teljesítmény (n), amelyre kiterjeszti a binomiális.,
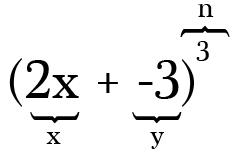
például a bővítéshez (2x-3)3, a két kifejezés 2x és -3, a teljesítmény, vagy n érték pedig 3. Ne feledje, hogy ha van egy kivonás a binomiális ez ó annyira fontos, hogy ne feledje, hogy tartalmazza a mínusz, mint egy negatív szimbólum a kísérő kifejezés.
a csodálatos dolog a binomiális tételben az, hogy lehetővé teszi számunkra, hogy megtaláljuk a kibővített polinomot anélkül, hogy egy csomó binomot megszoroznánk. Elég ügyes, nem?, Kiderül, hogy a kibővített polinom kifejezéseinek száma mindig egy több lesz, mint a kibővített hatalom. Ez azt jelenti, hogy létrehozunk egy polinomot 4 kifejezésekkel, mivel a példa ereje 3.
minden kifejezésnek lesz egy (2x) és (-3), valamint az “n choose k” képlete, ahol n=3. Ezt 4-szer írhatod le, minden egyes kifejezésre egyet, így a k érték “N” – ben marad, a hatalmak pedig egyelőre üresek.
ezután ki kell töltenie a k-értékeket és hatásköröket. Itt követheti az összegzési képletet, növelve az egyes kifejezések erejét., De elég könnyű követni a mintákat.
az “n” k értékei k=0-val kezdődnek, és minden ciklusban 1-gyel nőnek. Az utolsó kifejezésnek K-val egyenlő n-vel kell végződnie, ebben az esetben n = 3 és K=3.
ezután hozzá kell adnunk a hatásköröket (2x) és (-3).
a bekapcsolás (2x) az n-értékkel kezdődik, tehát ebben az esetben 3, minden ciklusban 1-gyel csökken, amíg nullára nem kerül. A bekapcsolás (-3) nullával kezdődik, majd minden alkalommal egy-egy alkalommal növekszik, amíg n-be nem jut, vagy 3 ebben a problémában.,

mivel a nulla teljesítményre emelt érték 1, egyszerűsítheti a feltételeket nulla erővel.

ezután folytassa a hatáskörök alkalmazását és egyszerűsítse, ahol csak lehetséges.,


az utolsó rész a kombinációs képlet megoldása. Ennek nyilvánvaló módja a kombinációk képletének alkalmazása minden problémára. De itt egy szép kis parancsikont fogunk használni Pascal Háromszögével.
Pascal háromszöge egy egyszerű, de erős háromszög, amelyet úgy alakítanak ki, hogy három 1-es háromszöget hoznak létre., Ezután minden sorhoz egyszerűen írja az 1-et mindkét végére, majd keresse meg a középső számot(eket) a két érték hozzáadásával közvetlenül felette.

most itt a jó rész. A Pascal háromszögében elrejtve minden válasz az “n choose k” – re! Ez olyan, mint egy titkos kis cheatsheet!
az alábbi ábra azt mutatja, hogy hol található a rejtett “n choose k”.,

problémánkhoz meg kell oldanunk: 3 válasszon 0-t, 3 Válasszon 1-et, 3 válasszon 2-t, 3 pedig válasszon 3-at. Ami az összes érték a 4.sorban. Tehát csak annyit kell tennünk, hogy megnézzük Pascal háromszögének 4. sorát, és összevetjük a válaszokat.
a 4. sor értéke: 1, 3, 3, 1. Tehát én csak helyettesíti a választ a mi n választani k.,

végül mindössze annyit kell tennie, hogy megszorozza és egyszerűsíti az egyes kifejezéseket a legegyszerűbb formájára. Ne felejtse el ellenőrizni a végső választ, hogy megbizonyosodjon arról, hogy az egyes kifejezések hatásköre továbbra is növeli-e az eredeti binomiális mértékét! Bízz bennem, hihetetlenül könnyű átírási hibát készíteni az ilyen típusú problémákban 😉
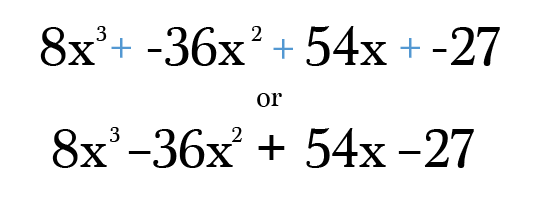
kell egy másik példa?,
a fenti videóban megmutatom, hogyan kell használni a binomiális tételt a binomiális (x – 3Y) ⁵ kibővítéséhez. Plusz mutatok néhány további trükköt a szervezett maradáshoz, valamint néhány gyors ellenőrzést, amellyel könnyen azonosíthatja a gyakori hibákat.
Köszönjük, hogy elolvasta!
❤ maradjon kapcsolatban ❤
legyen naprakész mindent matematikai Hacks akár!