
A Dirac delta függvény egy olyan funkció, bevezetett 1930-ban a P. A. M. Dirac, a híres könyv, a kvantummechanika. A Delta függvényt megjelenítő fizikai modell a véges teljes m tömeg eloszlása-az integrál a tömegeloszlás felett., Amikor az eloszlás egyre kisebb lesz, míg az M állandó, a tömegeloszlás egy ponttömegre zsugorodik, amelynek definíció szerint nulla mértéke van, mégis véges értékű integrálja egyenlő az M teljes tömeggel.
Heurisztikusan a Dirac delta függvény a Kronecker-delta kiterjesztésének tekinthető az integrált indexekből (a 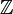 elemei) a valós indexekre (a
elemei) a valós indexekre (a 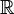 elemei)., Vegye figyelembe, hogy a Kronecker delta viselkedik, mint egy “szűrő” a összegzése:
elemei)., Vegye figyelembe, hogy a Kronecker delta viselkedik, mint egy “szűrő” a összegzése:
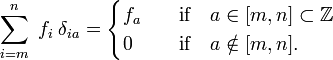
A hasonlat, a Dirac delta függvény δ(x−a) határozza meg (cserélje ki vagyok, az x pedig a összegzése vége egy integrációs x),
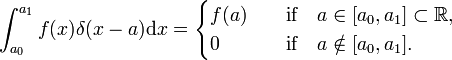
A Dirac delta függvény nem egy közönséges úriember térkép 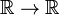 , de egy engedély, is ismert, mint egy helytelen vagy generalizált funkció. A fizikusok kifejezik különleges jellegét azzal, hogy kijelentik, hogy a Dirac delta funkciónak csak az integrand tényezőjeként van értelme (“az integrál alatt”)., A matematikusok azt mondják, hogy a delta funkció egy lineáris funkcionális térben teszt függvények.
, de egy engedély, is ismert, mint egy helytelen vagy generalizált funkció. A fizikusok kifejezik különleges jellegét azzal, hogy kijelentik, hogy a Dirac delta funkciónak csak az integrand tényezőjeként van értelme (“az integrál alatt”)., A matematikusok azt mondják, hogy a delta funkció egy lineáris funkcionális térben teszt függvények.
Tartalom
- 1 Tulajdonságok
- 2 Delta-konvergens sorozatok
- 2.1 Blokk funkciók
- 2.2 Gauss függvények
- 2.3 Lorentz-Cauchy funkciók
- 2.4 Sinc funkciók
- 3 Származékai a delta függvény
- 3.,1 A származék tulajdonságai
- 4 primitív
- 5 a Dirac delta függvény három dimenzióban
- 6 referenciák
tulajdonságok
leggyakrabban a delta függvény definíciójában az alsó és felső határ a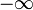 és
és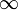 , ill. Innentől kezdve ez megtörténik.
, ill. Innentől kezdve ez megtörténik.
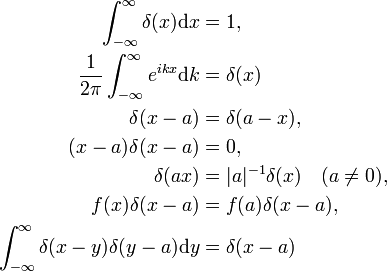
a fizikus ezen tulajdonságok igazolása az integrálba való megfelelő helyettesítéssel, az integrálszámítás szokásos szabályainak felhasználásával történik., Az F(x) = 1 (A második tulajdonság) egységfunkció Fourier-transzformációjaként a delta függvényt az alábbiakban mutatjuk be. Az utolsó tulajdonság a két identitásmátrix szorzatának analógiája,
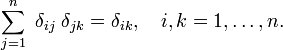
. 1. Blokk (“boxcar”) funkció(piros) alkalommal rendszeres funkció f (x) (kék).
Delta-konvergens szekvenciák
léteznek olyan fa(x) szabályos függvénycsaládok, amelyek családtagjai egyetlen α paraméter értékével különböznek egymástól., Egy ilyen család példáját a fa(x) = exp(−ax2) Gauss függvények családja alkotja, ahol az α egyetlen paraméter különböző értékei megkülönböztetik a különböző tagokat. Ha minden tag lineárisan normalizálható, azaz a következő integrál véges, tekintet nélkül α-ra,
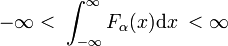
és minden tag x = 0 körül csúcsosodik, akkor a család delta-konvergens szekvenciát képezhet.,
Blokkfüggvények
a delta-konvergens szekvencia legegyszerűbb példáját a blokkfüggvények családja alkotja, amelyet pozitív Δ,
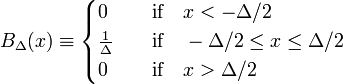
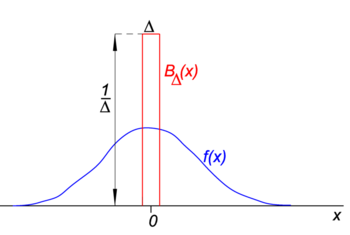
ábra. 1 a bδ blokkfunkció piros színnel jelenik meg. Nyilvánvaló, hogy a vörös görbe alatti terület (szélesség-magasság) egyenlő az egységgel, függetlenül a Δ értékétől,
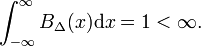
hagyja, hogy az önkényes függvény f (x) (kék az ábrán. 1) legyen folytonos (nincs ugrás) és véges az x=0 szomszédságában., Amikor a Δ nagyon kicsi lesz, és a blokkfüggvény nagyon keskeny (és szükségszerűen nagyon magas, mert a szélességi idő magassága állandó), az F(x) bδ(x) termék jó közelítéssel egyenlő f(0) BΔ(x) értékkel. Minél keskenyebb a blokk, annál jobb a közelítés., Ezért, Δ, hogy nulla,
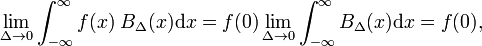
, amelyeket össze lehet hasonlítani a meghatározás, a delta függvény,
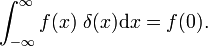
Ez azt mutatja, hogy a család blokk funkciók közelít a Dirac delta függvény csökkenő paraméter Δ; a család képezi a delta-konvergens sorozat:
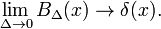
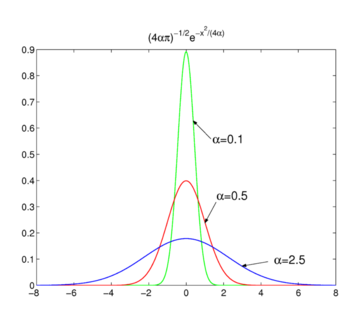
Ábra. 2. Gauss funkciók.
megjegyzés:az egész valós tengelyre integráltuk., Nyilvánvaló, hogy erre nincs szükség, kizárhattuk volna a blokkfüggvény nulla értékű szárnyait, és csak a középső púpra integráltuk − – Δ / 2-ről + Δ / 2-re. Matematikai szövegekben, például Ref. , ez a finomítás az integrációs határértékekben szerepel a delta-konvergens szekvencia meghatározásában. Vagyis szükség van arra, hogy a két szárny feletti integrálok eltűnjenek a határon. Mivel a fizikai alkalmazásokban előforduló delta-konvergens szekvenciák általában megfelelnek ennek a feltételnek, kihagyjuk a pontosabb matematikai meghatározást.,
Gauss függvények
Tekintsük a családot,
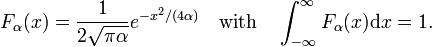
amint az az ábrán látható. 2 a függvények csúcsértéke x = 0 körül van, és szűkebbé válnak az α csökkenéséhez. Ezért a Gauss-függvények családja delta-konvergens szekvenciát alkot,
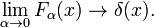
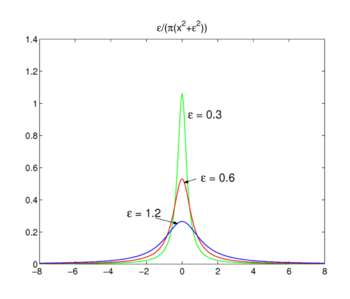
. 3. Lorentz-Cauchy függvények
Lorentz-Cauchy függvények
a függvénycsalád az ábrán látható., 3
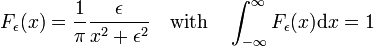
forms a delta-convergent sequence,
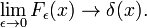
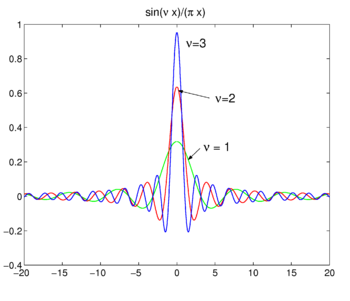
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4.
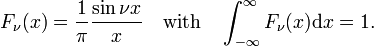
Ez a család összejön, hogy a delta függvény növekvő ν a pillanatnyi
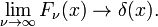
Ez a korlátozás könnyen vezet, hogy a Fourier-integrál ábrázolása a delta függvény:
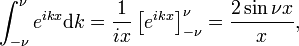
így
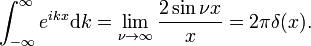
A Dirac delta függvény a Fourier az egység függvény f(x) = 1.
A delta függvény származékai
Vegyünk egy differenciálható F(x) függvényt, amely plusz-mínusz végtelenségig eltűnik.,d=”ed7dae11d6″>
ugyanúgy, mint a kvantummechanikai momentum operátor 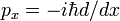 forgási szabályát és Hermiticitását bizonyítja, itt megmutattuk, hogy a D/dx Hermitian,
forgási szabályát és Hermiticitását bizonyítja, itt megmutattuk, hogy a D/dx Hermitian,
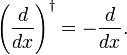
valóban, amikor az integrált belső termékként írjuk, részleges termékből következik a
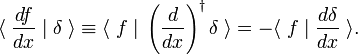
Ez a forgalmi szabály a delta függvény deriváltjának definíciója,
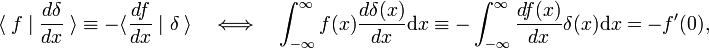
ahol a prím az F(X) első deriváltját jelöli., A delta függvény definíciója szerint az első származékot x = 0-ban értékeljük. A forgalmi szabály m-szeresének alkalmazásával következik, hogy a delta függvény mth-származékát a
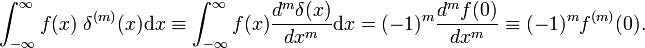
származék tulajdonságai
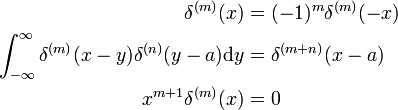
ezek az eredmények bizonyíthatók az x → −x helyettesítéssel és a d / dx forgalmi szabályának alkalmazásával (lásd fent).,
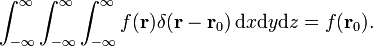
A három-dimenziós delta függvény lehet factorized
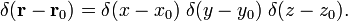
A gömb poláris koordináták
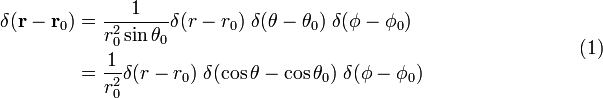
Bizonyíték egyenlet (1)
Írjon
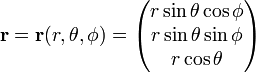
A Jacobi (Jacobi determináns) ez az átalakulás a Derékszögű koordináták, hogy gömb alakú poláris koordináták
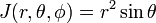
Fontolja
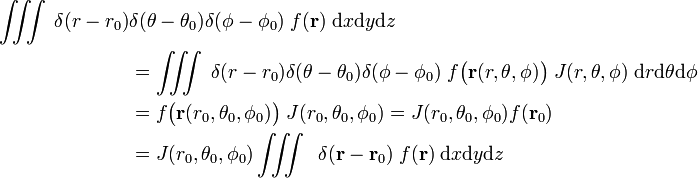
így
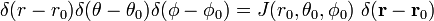
a
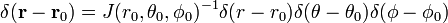
Az utolsó sort egyenlet (1) következik a lánc szabály.,
A következő hasznos, s gyakran alkalmazott ingatlan bebizonyították,
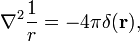
amennyiben ∇2 a Laplace operátor háromdimenziós Descartes-féle koordináták valamint a k a hossza, r.