logaritmikus függvények az exponenciális függvények inverzei. Az y = ax exponenciális függvény inverze x = ay. Az y = logax logaritmikus függvény az x = ay exponenciális egyenletnek felel meg. y = logax csak a következő feltételek mellett: x = ay, a > 0 és a≠1. Ezt logaritmikus függvénynek nevezik a bázissal.
fontolja meg, mit jelent az exponenciális függvény inverse: x = ay., Mivel az x szám és a bázis a, milyen teljesítmény y kell emelni egyenlő x? Ez az ismeretlen kitevő, y, egyenlő logax. Tehát látod, hogy a logaritmus nem más, mint egy kitevő. Definíció szerint, alogax = x, minden valós x > 0.
Az alábbiakban az y = logax forma ábrázolt grafikonjai láthatók, amikor a > 1 és amikor 0 < a < 1. Figyeljük meg, hogy a tartomány csak a pozitív valós számokból áll, és hogy a függvény mindig növekszik, ahogy x növekszik.,
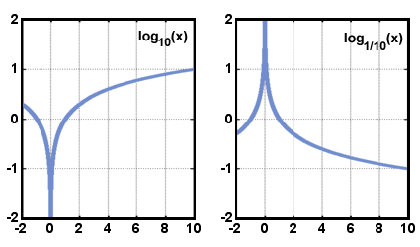
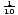 x.
x.a logaritmikus függvény tartománya a nullánál nagyobb valós szám, a tartomány pedig valós szám. Az y = logax gráf szimmetrikus az y = ax gráfjával az y = x vonalhoz képest. ez a kapcsolat minden függvényre és annak inverzére igaz.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(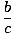 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
Egy természetes logaritmikus függvény logaritmikus függvény a bázis e. f (x) = logex = ln x, ahol x > 0. Ln x csak egy új formája a jelölés logaritmusok bázis e. a legtöbb számológépek gombok jelölt “log”és ” ln”. A” Napló “gomb feltételezi, hogy az alap tíz, az” ln ” gomb pedig természetesen lehetővé teszi az alap egyenlő e-t., A 10 bázisú logaritmikus függvényt néha közös logaritmikus függvénynek nevezik. Széles körben használják, mert számozási rendszerünk alapja tíz. A természetes logaritmusokat gyakrabban látják a kalkulusban.
két képlet létezik, amelyek lehetővé teszik a logaritmikus függvény alapjának megváltoztatását. Az első ezt állítja: logab = 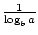 . Az alapváltoztatás híresebb és hasznosabb formuláját általában az alapképlet változásának nevezik. Ez lehetővé teszi, hogy a logaritmikus függvény alapja bármilyen pozitív valós számra ≠1 legyen. Azt állítja, hogy logax =
. Az alapváltoztatás híresebb és hasznosabb formuláját általában az alapképlet változásának nevezik. Ez lehetővé teszi, hogy a logaritmikus függvény alapja bármilyen pozitív valós számra ≠1 legyen. Azt állítja, hogy logax = 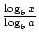 ., Ebben az esetben az A, b és x mind pozitív valós számok, és a, b≠1.
., Ebben az esetben az A, b és x mind pozitív valós számok, és a, b≠1.
a következő részben az exponenciális és logaritmikus függvények egyes alkalmazásait tárgyaljuk.