
elgondolkodott már azon, hogyan lehet hó a fagypont feletti hőmérsékleten? Nos, a naiv magyarázat az, hogy egyszerűen időbe telik, amíg a hópelyhek megolvadnak, miután behatolnak a fagyos levegő fölé, miközben lefelé leereszkednek a földre. Ez természetesen az oka annak, hogy a jégeső meleg időben eshet. Egyszerűen a jégeső kövek gyorsan esnek, túl gyorsan ahhoz, hogy a meleg levegő megolvassza a jégesőt. Ez azonban nem a fő magyarázat arra, hogy miért lehet hó, ha fagypont felett van.,
az alábbi ábrán látható, hogy egyértelműen függ a páratartalomtól – minél szárazabb, annál melegebb lehet havazáskor. Ez azt jelenti, hogy a fő tényező, legalábbis száraz körülmények között, a páratartalomhoz kapcsolódik. Ez a tényező a párolgás. Pontosabban, ahogy a hópelyhek leereszkednek, elpárolognak. Ez a folyamat hőt vesz fel, és hidegen tartja a pelyheket.
így, ha ki akarjuk számítani a maximális hőmérsékletet, meg kell becsülnünk a pehely nettó hőegyensúlyát. Először is, mivel a pelyhek meleg környezetben haladnak, a vezetésen keresztül hőt nyernek a környezetből., Másodszor, a hőt a pelyhek elpárologtatására használják, ezáltal hűtve őket. Ha a párolgási hő “mosogató” nagyobb, mint a hővezetés, a pelyhek fagyasztva maradnak.
kiderül, hogy ez könnyen kiszámítható. Nem, nem egyszerű kiszámítani a hővezetést vagy a párolgási hőt, de az arány, mivel különböző ismeretlen geometriai tényezők megszűnnek.
Ha nem érdekli a számítás (mert nem vagy tudományos torzszülött), egyszerűen látogasson el a számológép oldalra.
Ha érdekel, itt van a származtatás., Tegyük fel, hogy a pelyhek körüli áramlás olyan, hogy körülötte d szélességű határréteg alakul ki. A teljes hőáramlás $f_h$ a pehely (például, J/sec MKS) adja meg Fourier törvény:
ahol $\kappa $a hő diffúziós együtthatója levegő (pl., m2/sec MKS), c a hő kapacitása levegő (J/kg MKS), A felület a határfelületét a levegő.réteg a pehely körül, míg δt a pehely és a környezet közötti hőmérsékleti különbség.,
Hasonlóan lehet használni, Fick törvénye, hogy szerezze be a diffúzió a vízgőz a pehely (ahol a hőmérséklet fagypont közelében, a relatív páratartalom 100%), hogy a környezet, ahol a hőmérséklet magasabb a relatív páratartalom alacsonyabb:
itt D A Víz diffúziós együtthatója (pl. m2 / sec az MKS-ben), ρ pedig a vízgőz sűrűsége (kg/m3 az MKS-ben).,
a párolgó jég hőt igényel, így ha van egy vízgőz tömeg fluxus Φ a pehely, akkor szükség lenne hő sebességgel $f_w = \ epsilon \ Phi$ ahol $ \ epsilon$ a hő elpárologtatása jég (J / kg MKS).
a legmagasabb hőmérséklet, amely felett a hópehely megolvad, az a hőmérséklet, amelyre a két hőáramlás egyenlő:
vegye figyelembe, hogy a pehely körüli áramlás geometriája megszűnik, mivel mindkét hőáramlás ugyanúgy függ a d-től és az A-tól., Ez akkor is így lenne, ha a pehely körüli határréteg olyan összetett, hogy a d valójában az iránytól függ. Ezért
ahol $ \ rho_{sat}$ a telítettség vízgőz sűrűsége.
A számok beillesztése (amely megtalálható például a kémia és fizika CRC kézikönyvében), a hőmérséklet implicit egyenletét eredményezi, mivel a telítettség vízgőz sűrűsége a hőmérséklettől is függ., Egyszerűsíthetjük a dolgokat, ha ehelyett megkérdezzük, hogy mi a relatív páratartalom ahhoz, hogy a pehely fagyott maradjon egy adott hőmérsékleten. Ez:
ahol $t_c$ a hőmérséklet Celsius fok.
Ez a funkció az alábbi ábrán látható, Matsuo és Sasyo 1981-es adataival együtt. Amint az az ábrán látható, a számított grafikon nagyjából az alsó határ, amely alatt nincs eső. Melegebb hőmérsékleten keverék van., Az olvadásmentes vonal felett 1°C-ig többnyire hó, míg a vonal felett 1°C és 2°C között többnyire eső, de hó is lehet. Ezek az események további hatások, például erős leépítések, a hó olvadásához szükséges idő stb.
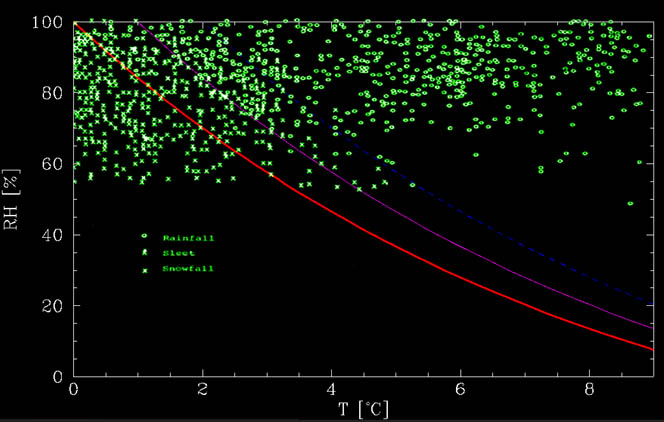
így, ha meleg időjárási havat akarunk megfigyelni, nagyon száraz körülmények szükségesek. Például, ha a talaj páratartalma csak körülbelül 20% (Nagyon ritka, mert ha csapadék van, a légkör általában nedves!) ezután 8°C-on (vagy 46°F-on az angol felhasználók számára) havazhat.,
egy másik követelmény, hogy az ereszkedés mentén sehol sem haladja meg a levegő az olvadásmentes vonalat. Ha igen, a pehely természetesen megolvad.
Ha a hőmérséklet fagypont fölé emelkedik, nincs olyan paraméter, amellyel a csapadék típusát meg lehet határozni a bizonyosság érdekében. Csak azt tudjuk megjósolni, hogy a hó valóban esik-e. Ezt a häggmark és Ivarsson (1997) eredményei alapján lehet elvégezni, csak a fagyott izzó használatára korrigálva, nem pedig a nedves izzó hőmérsékletére.
a lényeg egy számológép,amellyel a hó valószínűsége becsülhető.,