keresztmetszetek

területek tulajdonságai

Centroid

az alakzat centroidja azt a pontot jelöli, amelyről a szakasz területe egyenletesen oszlik el. Ha a terület kétszeresen szimmetrikus két ortogonális tengely körül, akkor a centroid ezen tengelyek metszéspontjában fekszik. Ha a terület csak egy tengely körül szimmetrikus, akkor a centroid valahol a tengely mentén fekszik (a másik koordinátát ki kell számítani)., Ha a pontos helyét a elrejtve középen nem lehet által meghatározott ellenőrzés lehet kiszámítani:

amennyiben ügyész képviseli a terület egy elképzelhetetlenül csekély elem, a teljes terület a keresztmetszet, s x, y koordinátáit elem dA tekintetében a tengely az érdeklődés.,

a közös keresztmetszetek centroidális helyei jól dokumentáltak, ezért általában nem szükséges kiszámítani a helyet a fenti egyenletekkel., azon alapalakzatok közül, amelyek centroid helyei bizonyos referenciapont tekintetében ismertek,akkor az összetett keresztmetszet centroidális helye a következőképpen számítható ki:

ahol XC,i és YC, az I.szakasz centroidális helyének téglalap alakú koordinátái a referenciapont tekintetében, az AI pedig az I. szakasz területe.,

Centroidális távolság

a centroidális távolság, c, a keresztmetszet centroidjától a szélsőséges szálig terjedő távolság., A centroidal távolság az y-irányban egy téglalap keresztmetszetű mutatja az alábbi ábra:

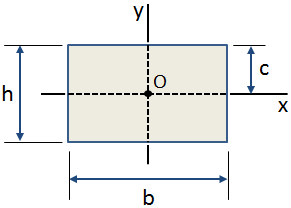
Közös használ a centroidal távolság a következők:

• számító, a maximális hajlító stressz-keresztmetszet
• érték kiszámításakor az első pillanatban, terület, Q, a fenti pont a keresztmetszet meghatározása a nyírási feszültség, hogy pont

az Első Pillanatban Terület

Az első pillanatban olyan terület vonatkozásában, egy tengelye kamat számítása a következőképpen történik:

Qx = ∫ y dA

Qy = ∫ x dA

amennyiben Qx az első pillanatban az x-tengely, Qy az első pillanatban az y-tengely.,Ha a terület álló gyűjteménye alapvető formák, akinek centroidal helyeken ismert tekintetében a tengely a kamat, akkor az első pillanatban a kompozit területén lehet számítani, mint:

Megjegyezzük, hogy az első pillanatban a területen használják kiszámításakor a súlypontja a keresztmetszete tekintetében néhány eredetű (mint arról korábban már volt szó)., Az első pillanatot a nyírófeszültség értékének kiszámításakor is használják a keresztmetszet egy adott pontján. Ebben az esetben az első pillanatot olyan területre kell kiszámítani, amely a keresztmetszet kisebb részét teszi ki, ahol a területet az érdeklődési pont és a keresztmetszet szélsőséges rostja (felső vagy alsó) határolja. Az első pillanatot egy olyan tengely körül számítják ki, amely áthalad a keresztmetszet centroidján.,

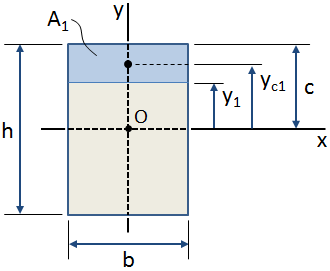
a fenti ábrán az árnyékos kék terület a teljes keresztmetszet érdeklődési területe.,nt ezen a területen a tekintetben, hogy az x-tengely (amely áthalad a keresztmetszet elrejtve középen, O pont a fenti ábrát) az alábbiak szerint kell kiszámítani:

Ha a centroidal helyét az érdeklődési területe ismert, aztán az első pillanatban a terület tekintetében a tengely lehet kiszámítani, mint (lásd a fenti ábrát):

Meg kell jegyezni, hogy az első pillanatban, hogy egy terület lesz pozitív vagy negatív, attól függően, hogy a helyzet a helyzetben a terület tekintetében a tengely az érdeklődés., Ezért a keresztmetszet teljes területének első pillanata a saját centroidjához képest nulla lesz.

terület Tehetetlenségi nyomaték

a terület második pillanata, ismertebb nevén a tehetetlenség pillanata, I, egy keresztmetszet azt jelzi, hogy a szerkezeti tag képes ellenállni a hajlításnak.,(Megjegyzés: 1) a Ix., valamint Iy azok a pillanatok, amikor a tehetetlenség miatt az x – y – tengely, illetve számítja ki:

Ix = ∫ y2 dA

Iy = ∫ x2 dA

ahol x, y koordinátáit elem dA tekintetében a tengely az érdeklődés.

leggyakrabban a tehetetlenségi pillanatokat a szakasz centroidjához viszonyítva számítják ki. Ebben az esetben a tehetetlenség centroid pillanatainak nevezik őket, és az X tengely körüli tehetetlenségre Icx-ként, az y tengely körüli tehetetlenségre pedig ICX-ként jelölik őket.,

a közös keresztmetszetek tehetetlenségi pillanatai jól dokumentáltak, ezért általában nem szükséges kiszámítani őket a fenti egyenletekkel. Az oldal végén több közös keresztmetszet tulajdonságai vannak megadva.

Ha egy keresztmetszet olyan alapformák gyűjteményéből áll, amelyek centroidjai egybeesnek, akkor az összetett szakasz tehetetlenségi pillanata egyszerűen a tehetetlenség egyes pillanatainak összege. Erre példa egy dobozsugár, amely két téglalap alakú részből áll, az alábbiak szerint., Ebben az esetben a külső rész “pozitív területtel”, a belső rész “negatív területtel” rendelkezik, tehát a tehetetlenségi összetett pillanat a belső szakasz tehetetlenségi nyomatékának kivonása a külső szakaszból.

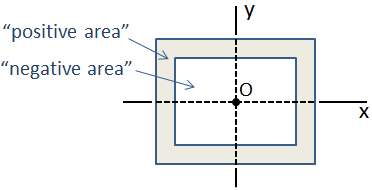
bonyolultabb összetett keresztmetszet esetén, amelyben a centroid helyek nem egybeesnek, a tehetetlenségi nyomaték kiszámítható a párhuzamos tengely tételével.

fontos, hogy ne keverjük össze egy terület tehetetlenségi pillanatát egy szilárd test tehetetlenségi tömegével., A terület tehetetlenségi nyomatéka a keresztmetszet hajlítási ellenállását jelzi, míg a tehetetlenségi tömegpont a test forgásállóságát jelzi.,

Párhuzamos Tengely Tétel

Ha a tehetetlenségi nyomaték a keresztmetszet egy centroidal tengely ismert, akkor a párhuzamos tengely tétel kiszámításához használható a tehetetlenségi nyomaték bármilyen párhuzamos tengely:

amennyiben Ic a tehetetlenségi nyomaték a centroidal tengely, d a távolság a centroidal tengely, valamint a párhuzamos tengely, valamint a terület a keresztmetszet.,

Ha egy keresztmetszet olyan alapformák gyűjteményéből áll, amelyek centroid tehetetlenségi pillanatai ismertek a centroidok távolsága mellett egy referenciapontig, akkor a párhuzamos tengely tétel felhasználható a kompozit keresztmetszet tehetetlenségi pillanatának kiszámításához.

például egy I-gerenda közelíthető 3 téglalappal, az alábbiak szerint. Mivel ez a kompozit szakasz szimmetrikus mind az x -, mind az y – tengelyek tekintetében, a szakasz középpontja ellenőrzéssel helyezhető el ezen tengelyek metszéspontjában. A centroid a származási helyen található, O, az ábrán.,

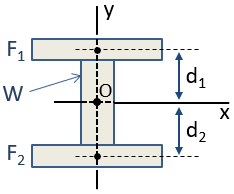
az összetett szakasz tehetetlenségi pillanatát a párhuzamos tengely tételével lehet kiszámítani. Az X tengely körüli centroid tehetetlenségi nyomatékot, az Icx-et a következőképpen számítjuk ki:

ahol az Icx kifejezések az egyes szakaszok tehetetlenségének pillanatai a saját centroidjaikról az x tengely tájolásában, a d kifejezések az egyes szakaszközpontok távolsága az összetett szakasz centroidjához, az a kifejezések az egyes szakaszok területei. Mivel a W szakasz centroidja és a kompozit szakasz centroidja egybeesik, a D az adott szakaszra nulla, tehát nincs Ad2 kifejezés.,

fontos megjegyezni a párhuzamos tengely tétel implikációját, hogy mivel az egyes szakasz távolabb mozog a kompozit szakasz középpontjától, az adott szakasz hozzájárulása az összetett szakasz tehetetlenségi pillanatához D2 tényezővel növekszik. Ezért, ha a szándék egy adott tengely körüli szakasz tehetetlenségi nyomatékának növelése, akkor a leghatékonyabb a területet a lehető legtávolabb elhelyezni a tengelytől. Ez magyarázza az I-gerenda alakját., A karimák a tehetetlenségi nyomaték elsődleges hozzájárulói, a web pedig a karimák elválasztását szolgálja a hajlítási tengelytől. A webnek azonban bizonyos vastagságot kell fenntartania a csatok elkerülése érdekében, valamint azért, mert a web a nyírási stressz jelentős részét veszi igénybe a szakaszban.

poláris Tehetetlenségi nyomaték

a keresztmetszet I poláris tehetetlenségi nyomatéka azt jelzi, hogy a szerkezeti elem képes ellenállni a szakaszra merőleges tengely körüli torzításnak., A polar tehetetlenségi nyomaték egy rész tekintetében egy tengely mentén lehet kiszámítani, hogy:

ahol x, y koordinátáit elem dA tekintetében a tengely kamatot r a távolság az elem dA a tengely az érdeklődés.,

bár a poláris tehetetlenségi nyomatékot a fenti egyenlet segítségével lehet kiszámítani, általában kényelmesebb a merőleges tengely tételével kiszámítani, amely kimondja, hogy egy terület poláris tehetetlenségi nyomatéka a tehetetlenségi pillanatok összege bármely két ortogonális tengelyen, amelyek áthaladnak az érdeklődési tengelyen:

leggyakrabban a kamat tengelye áthalad a tengelyen.a keresztmetszet centroidja.,

szakasz Modulus

a gerenda maximális hajlítási feszültségét σb = Mc / Ic-ként számítják ki, ahol c a semleges tengelytől a szélsőséges szálig terjedő távolság, Icis a tehetetlenség centroidális pillanata, M pedig a hajlítási pillanat. A keresztmetszeti modulus egyesíti a c Ic feltételek a hajlító stressz egyenlet:

az a rész modulus, a hajlító stressz számított, mint σb = M / S. A segédprogram a szakasz modulus, hogy jellemzi a hajlítási ellenállás a keresztmetszet egyetlen kifejezés., Ez lehetővé teszi a gerenda keresztmetszetének optimalizálását, hogy ellenálljon a hajlításnak egyetlen paraméter maximalizálásával.

Gyrálás sugara

a gyrálás sugara azt a távolságot jelenti egy szakasz centroidjától, amelyen az egész terület koncentrálható anélkül, hogy bármilyen hatással lenne a tehetetlenség pillanatára.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

a Tulajdonságok a Közös keresztmetszet

Az alábbi táblázat a tulajdonságok a közös keresztmetszet. A felsorolt referenciákban részletesebb táblázatok találhatók.

a táblázatban kiszámított tulajdonságok közé tartozik a terület, a centroidális tehetetlenségi nyomaték, a szekció modulusa és a gyrálás sugara.,