ezeken az oldalakon néhány érdekes fogalmat nézünk meg, megnézzük az ívelt teret:mit jelent az ívelt tér, hogyan tudjuk megmondani, hogy egy tér ívelt-e belülről vagy kívülről.
megnézzük, hogyan lehet beágyazni a tér típusát egy másikban, és látjuk, hogy különböző terek között különböző módon tudunk térképezni.
azt is vizsgáljuk, hogyan tudunk végtelenül nagy és végtelenül kis vektorokat reprezentálni a tereinkben olyan módon, amely nem vezet szingularitásokhoz és egyéb problémákhoz.,
ezek a fogalmak hasznosnak bizonyulnak, még akkor is, ha lapos térrel dolgozunk, megtaláljuk a vektorok és síkok ábrázolásának módját, amelyek nem mennek át az eredeten. Ez lehetőséget ad arra, hogy egyetlen műveletként ábrázoljuk a forgatásokat és fordításokat.
a másik alkalmazás relativisztikus téridő.
Rienmannian Geometria
A Rienmannian geometria tér görbe különböző helyeken (lásd a házakat) itt megnézzük geometriák, ahol a görbe a tér állandó.,
Eulidean Geometria
lapos tér
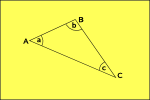
a Hiperbolikus Geometria
a tér görbe passzív
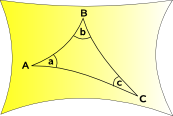
Szférikus Geometria, Elliptikus Geometria
a tér görbe befelé
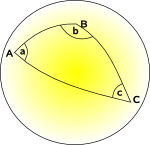
A hajlított (Nem-Euklideszi) geometria nem találjuk meg a koordinátákat, amelyek egymásra merőleges, ahol a koordináta vonalak párhuzamosak egymással, s hol minden rács négyzet van ugyanazon a területen., Lehet, hogy találunk egy koordináta-rendszert, ahol meg tudjuk csinálni ezeket, de nem mindet.
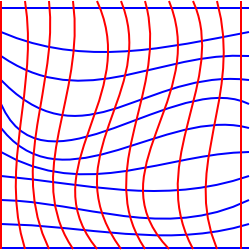
Ez a diagram megpróbálja szemléltetni ezt a helyzetet 2 dimenzióban, bár kissé félrevezető, mert egy síkra rajzoltuk, hogy téglalap alakú koordinátákat rajzolhassunk.
egy olyan helyzet szemléltetésére, ahol ez lehetetlen, egy kétdimenziós síkra gondolhatunk, amelyet a harmadik dimenzióba feszítettek.,

ebben a helyzetben kiválaszthatjuk azokat a koordinátákat, amelyek téglalap alakú rácsot alkotnak, amikor egy vízszintes síkra vetítik, azonban a felszínen élő személynek, akkor a rács négyzeteinek egy része nagyobb területűnek tűnik, mint mások, és a rácsvonalak nem tűnnek párhuzamosnak. Nincs olyan kétdimenziós koordináta-rendszer, amely egyszerre őrizné meg a párhuzamos vonalakat, szögeket és területeket.,
hasonló példa próbálja feltérképezni a Föld felszínét, használhatunk szélességi és hosszúsági vonalakat, de a hosszúsági vonalak közelebb kerülnek a pólusokhoz.
ezekben az esetekben a 3 dimenziós koordináták tekintetében dolgozhatunk, és ez egy olyan megközelítés, amelyet bizonyos típusú nem-euklideszi geometriákkal fogunk alkalmazni. Gyakran lehet beágyazni egy adott geometriát egy magasabb dimenziós geometriába annak érdekében, hogy euklideszi legyen.,
néha előfordul, hogy amikor egy nagy léptékű geometriát vizsgálunk, akkor nem euklideszi, de ha kisebb-kisebb léptékben nézzük, akkor közelít egy euklideszi geometriához. Ehhez meg kell találnunk egy koordináta-rendszert, ahol a szögek minden ponton megmaradnak, vagyis a vízszintes és függőleges koordináta-vonalaknak mindig 90° – on kell metszeniük, annak ellenére, hogy a vonalak nem egyenesek. Ez az úgynevezett konform geometria. Az ilyen típusú geometriában legalább egy helyi koordináta-rendszert definiálhatunk.,
ehhez kapcsolódik, hogy a geometria differenciálható-e és integrálható-e, ennek feltétele, hogy jól viselkedjen, és ne legyen hirtelen ugrása stb. Egyes geometriák és koordináta-rendszerek bizonyos helyeken jól viselkedhetnek, de szingularitásúak stb.
a görbület mérésének módjáról szóló megbeszéléshez lásd ezt az oldalt.
matematikai jelölés
hogyan kezeljük a geometriákat, ahol nem tudjuk használni az euklideszi geometriára vonatkozó összes szabályt?,
az egyik megközelítés a tenzor jelölés használata, ez olyan konvenciókat és jelöléseket biztosít, amelyek segítenek a különböző koordináta-rendszerek közötti váltásban. Egy ortogonális koordináta-rendszer, helyi bármely pont, lehet meghatározni alapján Vektorok, amelyek érintői a koordináta vonalak.,Sokrétű
látod ez az oldal
Kapcsolat Hiperbolikus, valamint Minkowski Geometriák
| Minkowski-Geometria | Hiperbolikus Geometria | |
| pont | esemény tér-idő | részecske az egyenletes mozgás |
| távolság két pont között | a tér-idő intervallum között két esemény | relatív sebesség között két ilyen részecskék |
Terminológia
Itt megnézzük a terminológia mint a geometriák, terek, modellek, előrejelzések, majd átalakítja., Meglehetősen nehéz, amikor nem euklideszi geometriákkal foglalkozunk, mert hasonló terminológiát használunk, mint a hagyományos euklideszi térben, de a kifejezések kissé eltérő tulajdonságokkal rendelkezhetnek.,próbáld
Elliptikus Geometria
Modellek
Példa:
- Felső fele-repülő modell
- Poincare disc modell
- Projektív modell
- Konformális modell
Előrejelzések
sztereografikus
Átalakítja
Invariáns
Példa:
- Möbius Átalakítani
- Lorentz Transzformáció
Párhuzamos Posztulátum
Ha elvesszük a párhuzamos posztulátum a Euklideszi Térben.,
Ez a következőhöz vezet:
- párhuzamos posztulátum hamis
- a háromszög szögei nem adnak hozzá π
- egy adott méretű alakhoz, általában nem létezik hasonló, nagyobb méretű alak.,aktív
konformális (Poincaré lemez ) egyenes vonalak – geodesics szegmensek körök angle megőrzése több belső szögeit, háromszög π-(α+β+γ)=CΔ távolság két pont között a