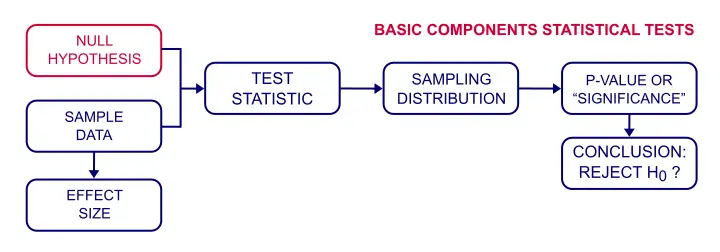
A null hipotézis pontos kijelentés egy populációról, amelyet megpróbálunk elutasítani a mintaadatokkal.Általában nem hisszük, hogy a null hipotézisünk (vagy H0) igaz. Szükségünk van azonban néhány pontos kijelentésre, mint a statisztikai szignifikancia tesztelés kiindulópontjára.
Null hipotézis példák
gyakran-de nem mindig – a null hipotézis azt állítja, hogy nincs összefüggés vagy különbség a változók vagy szubpopulációk között., Így, néhány tipikus null hipotézisek a következők:
- az összefüggés frusztráció, agresszió nulla (korreláció-analízis);
- az átlagos jövedelem a férfiak, mint a nők (független minták t-teszt);
- Állampolgárság (tökéletesen) független zenei preferencia (chi-négyzet függetlenség-vizsgálat);
- az átlagos népesség jövedelem egyenlő volt vége 2012, 2016-ra (ismételt intézkedések ANOVA).
” Null “nem jelenti a”nulla “
általános félreértés, hogy” null “azt jelenti,”nulla”. Ez gyakran, de nem mindig így van., Például egy null hipotézis azt is kijelenthetia frusztráció és az aggresszió közötti korreláció 0.5.No zéró érintett itt – bár kissé szokatlan-tökéletesen érvényes.
A” null “A” null hipotézis “származik”nullify” 5: A null hipotézis az a kijelentés, hogy megpróbáljuk megcáfolni, függetlenül attól, hogy nem (nem) adja meg a nulla hatás.
Null hipotézis tesztelés-hogyan működik?
szeretném tudni, hogy a boldogság kapcsolódik-e a holland emberek gazdagságához. Az egyik megközelítés ennek kiderítésére egy null hipotézis megfogalmazása., Mivel a” kapcsolódó ” nem pontos, az ellenkező kijelentést választjuk null hipotézisünkként: a gazdagság és a boldogság közötti korreláció nulla az összes holland ember között.Most megpróbáljuk megcáfolni ezt a hipotézist annak bizonyítására, hogy a boldogság és a gazdagság összefügg egymással.
most nem tudjuk ésszerűen megkérdezni mind a 17 142 066 Holland embert, mennyire boldogok általában.

ezért kérünk egy mintát (mondjuk 100 embert) a gazdagságukról és boldogságukról. A boldogság és a gazdagság közötti összefüggés 0,25 a mintánkban., Most már van egy probléma: minta eredmények általában némileg eltérnek populáció eredmények. Tehát ha a korreláció valóban nulla a lakosságunkban, akkor nem nulla korrelációt találhatunk a mintánkban. Ennek a fontos pontnak a szemléltetéséhez vessen egy pillantást az alábbi szórólapra. Az N = 200 teljes népessége számára a boldogság és a gazdagság közötti nulla összefüggést jeleníti meg.

most egy n = 20 véletlenszerű mintát rajzolunk ebből a populációból (a korábbi scatterplot piros pontjai). Annak ellenére, hogy a népesség korreláció nulla, találtunk egy megdöbbentő 0.,82 korreláció a mintánkban. Az alábbi ábra ezt szemlélteti azáltal, hogy kihagyja az összes nem mintavételezett egységet a korábbi szórásképünkből.

Ez felveti azt a kérdést, hogy hogyan mondhatunk bármit a lakosságunkról, ha csak egy apró minta van belőle. Az alapvető válasz: ritkán mondhatunk semmit 100% – os bizonyossággal. Azonban sokat mondhatunk 99%, 95% vagy 90% bizonyossággal.
valószínűség
tehát hogyan működik ez? Nos, alapvetően, néhány minta kimenetele nagyon valószínűtlen, tekintettel a null hipotézisünkre., Mint így, az alábbi ábra a különböző mintakorrelációk valószínűségeit mutatja (N = 100), ha a populáció korrelációja valóban nulla.

egy számítógép könnyen kiszámítja ezeket a valószínűségeket. Ehhez azonban szükség van egy mintaméretre (esetünkben 100) és egy feltételezett populációs korrelációra (esetünkben 0). Ezért van szükségünk egy null hipotézisre.
Ha megnézzük, hogy ez a mintavételezési engedély gondosan, azt látjuk, hogy a minta összefüggések körül, 0 leginkább: egy 0.68 valószínűsége, hogy találjunk egy összefüggés -0.1 pedig 0.1. Mit jelent ez?, Nos, ne feledje, hogy a valószínűségek relatív frekvenciáknak tekinthetők. Képzeljük el, hogy 1000 mintát vonunk le a meglévő helyett. Ez 1000 korrelációs együtthatót eredményezne, ezek közül mintegy 680-0,68-as relatív gyakoriság -0,1-0,1 tartományban lenne. Hasonlóképpen 0,95 (vagy 95%) a valószínűsége annak, hogy a minta korrelációt talál -0,2 és 0,2 között.
p-értékek
0, 25-ös minta korrelációt találtunk. Mennyire valószínű, hogy ha a népesség korrelációja nulla?, A válasz p-értékként ismert(a valószínűségi érték rövidítése): a p-érték annak a valószínűsége, hogy valamilyen minta eredményt vagy szélsőségesebb eredményt talál, ha a null hipotézis igaz.Tekintettel a 0, 25 korrelációra, a” szélsőségesebb ” általában 0, 25-nél nagyobb vagy -0, 25-nél kisebb. Nem tudjuk megmondani a grafikonunkból, de a mögöttes táblázat azt mondja nekünk, hogy p ≈ 0.012. Ha a null hipotézis igaz, akkor 1,2% a valószínűsége annak, hogy megtaláljuk a minta korrelációját.
következtetés?
Ha a populációs korrelációnk valóban nulla, akkor 0, 25-ös minta korrelációt találunk N = 100 mintában., Ennek valószínűsége csak 0,012, tehát nagyon valószínűtlen. Ésszerű következtetés az, hogy a népesség-korreláció végül sem volt nulla.
következtetés: elutasítjuk a null hipotézist. A mintaeredmény alapján már nem hisszük, hogy a boldogság és a gazdagság nem függ össze egymással. Ezt azonban még mindig nem tudjuk biztosan kijelenteni.
Null hipotézis-korlátozások
eddig csak arra a következtetésre jutottunk, hogy a populáció korrelációja valószínűleg nem nulla. Ez az egyetlen következtetés a mi null hipotézis megközelítés, és ez nem igazán olyan érdekes.,
amit igazán tudni akarunk, az a népesség korrelációja. A 0,25-ös minta korrelációja ésszerű becslésnek tűnik. Egy ilyen számot pontbecslésnek nevezünk.
most egy új minta eltérő korrelációval állhat elő. Érdekes kérdés, hogy a minta korrelációink mennyire ingadoznának a mintákon, ha sok közülük rajzolnánk. Az alábbi ábra pontosan ezt mutatja, feltételezve, hogy a minta mérete N = 100 és a (pont) becslés 0,25 a népesség korreláció.,

Konfidencia-Intervallum
A minta eredmény azt sugallja, hogy valami 95% – a sok-sok mintát kell egy összefüggés 0.06 pedig 0.43. Ezt a tartományt konfidencia intervallumnak nevezik. Bár nem pontosan helyes, ez a legkönnyebben bár a sávszélesség, amely valószínűleg mellékeli a lakosság korreláció.
egy dolog megjegyezni, hogy a concidence intervallum meglehetősen széles. Szinte nulla korrelációt tartalmaz, pontosan azt a nullhipotézist, amelyet korábban elutasítottunk.,
Egy másik dolog, amit meg kell jegyezni, hogy a mintavételi eloszlásunk és a konfidencia intervallumunk kissé aszimmetrikus. Szimmetrikusak a legtöbb más statisztikához (például eszközök vagy béta együtthatók), de nem korrelálnak.